5 Ways to Master Adjacent and Vertical Angles

Understanding the intricacies of geometry can be both a fascinating and rewarding journey, especially when diving into the fundamental concepts such as adjacent angles and vertical angles. These terms might sound intimidating at first, but once you grasp their essence, you unlock a new layer of understanding spatial relationships that can make complex geometrical problems much more manageable. In this article, we will explore five strategic methods to master adjacent and vertical angles, ensuring you not only comprehend these concepts but can apply them with confidence.

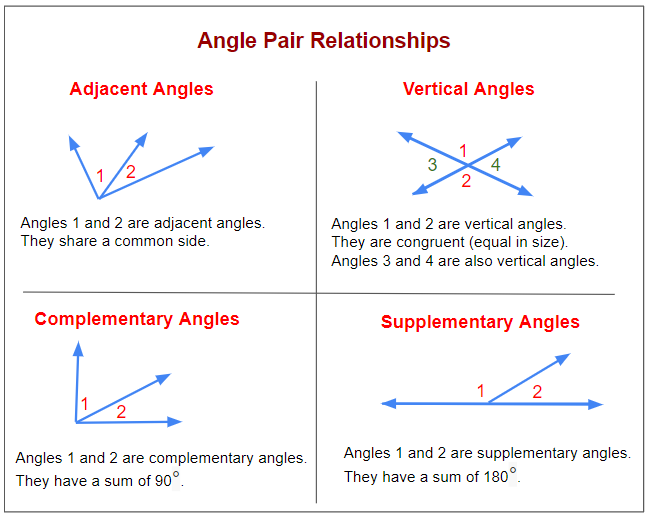
Understanding Adjacent Angles

Before diving into mastering adjacent angles, let's define what they are. Adjacent angles are two angles that have:

• A common vertex
• A common side
• No overlap

Here's how to get a grip on adjacent angles:

1. Visualize the Common Side

To better understand adjacent angles, always visualize the shared side, or “arm”, as a dividing line between two angles. This visualization:

• Makes it easier to recognize angles that are adjacent.
• Helps in identifying how angles relate to each other.

2. Utilize the Sum Property

Adjacent angles often share a sum relationship:

• If two adjacent angles form a straight line, their sum will be 180 degrees.
• Use this property to solve for unknown angles by knowing that if one angle is given, the adjacent angle can be found.

📚 Note: Adjacent angles do not always sum to 180 degrees. They form linear pairs when they do.

3. Practice Identifying in Various Geometrical Figures

Look for adjacent angles in:

• Triangles
• Quadrilaterals
• Circles, around the circumference

Practicing with different geometric figures strengthens your understanding of where adjacent angles might appear.

4. Sketch and Label Angles

Physical or digital sketching can help:

• Create diagrams to illustrate where adjacent angles exist.
• Label each angle to see the relationships more clearly.

5. Use Real-World Examples

Apply your knowledge to real-life scenarios:

• Building corners
• The angles between crossing roads
• Open books or notebooks

This makes abstract geometry more tangible and relatable.

Understanding Vertical Angles

Vertical angles, or opposite angles, are a bit more straightforward once you understand their properties:

• Formed by two intersecting lines
• They are opposite each other
• They are congruent (equal in measure)

Here are strategies to master vertical angles:

1. Visualize the Cross

Always imagine or draw two intersecting lines:

• The point of intersection creates four angles.
• The pairs opposite to each other are vertical angles.

2. Recognize the Equality

Vertical angles are always equal:

• If one vertical angle is known, its opposite will be the same.
• This principle is vital for solving problems and can simplify complex geometric setups.

3. Engage in Problem Solving

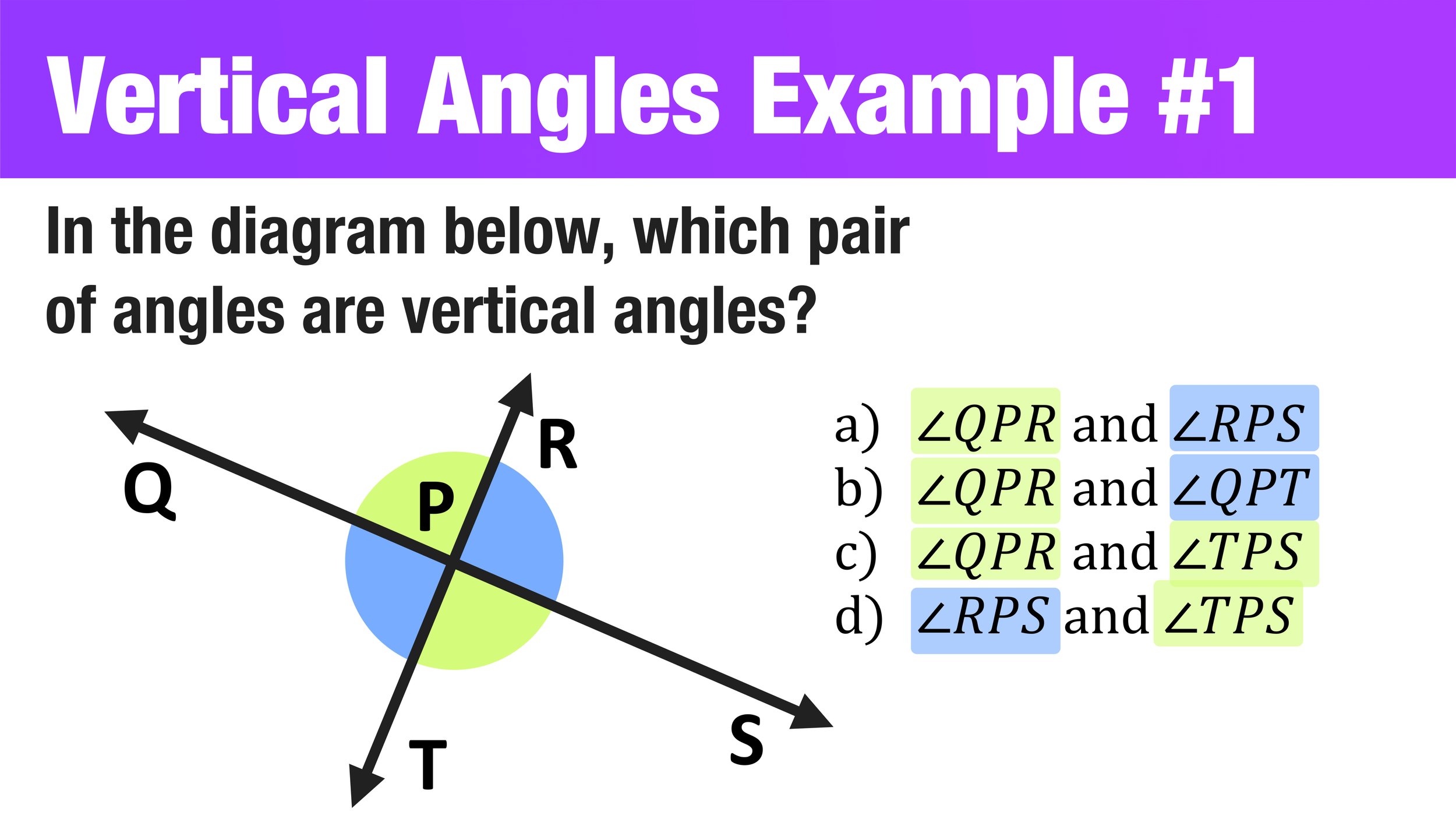
Practice by solving problems involving vertical angles:

• Given one angle, find its vertical counterpart.
• Use vertical angles to solve for other angles in a geometric figure.

4. Use Vertical Angles in Conjunction with Other Properties

Combine the understanding of vertical angles with:

• Supplementary angles (angles that sum to 180 degrees)
• Complementary angles (angles that sum to 90 degrees)
• Linear pairs (adjacent angles that sum to 180 degrees)

This integration helps in tackling complex angle relationships.

5. Relate to Real-Life Situations

Observe vertical angles in everyday life:

• Intersection of highways or streets
• Scissors’ open position
• An open ladder leaning against a wall

This practical observation reinforces your understanding and memory.

Mastering adjacent and vertical angles requires a blend of theoretical knowledge and practical application. By breaking down these concepts into digestible strategies, you empower yourself to confidently tackle geometrical problems, enhancing your spatial reasoning skills. Remember, geometry isn't just about understanding shapes; it's about understanding how the world around us is structured and interconnected.