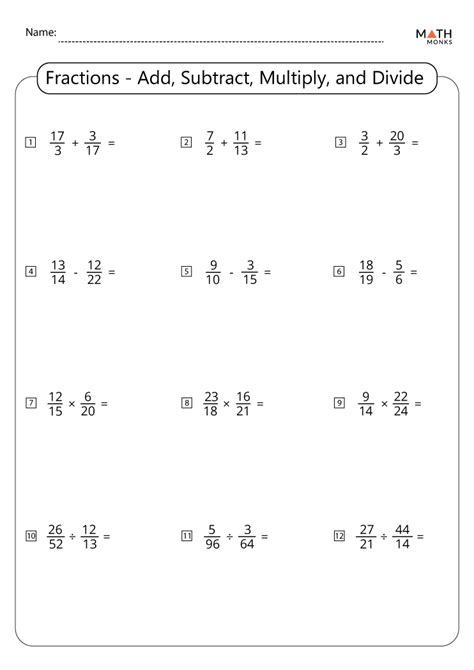
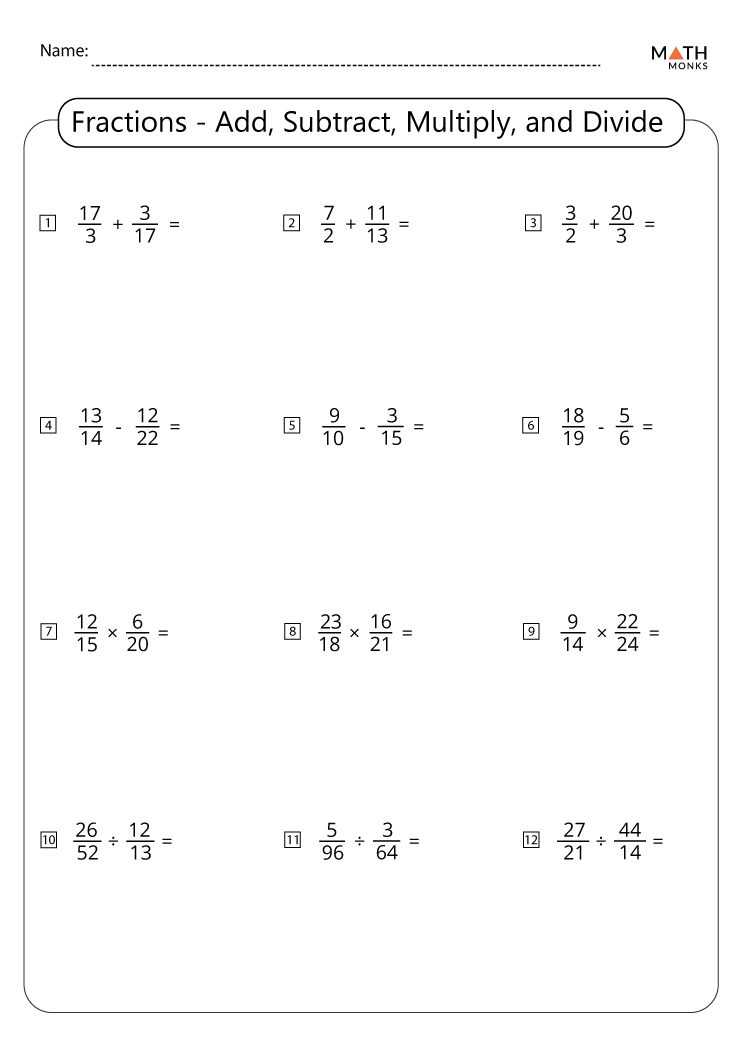
Fractions Worksheet: Add, Subtract, Multiply, Divide Made Easy
Fractions Worksheet: Simplifying the Process of Adding, Subtracting, Multiplying, and Dividing
Learning to work with fractions can be a challenging task, especially for young students. However, with the right tools and practice, mastering fractions can become a breeze. In this article, we will provide a comprehensive guide on how to add, subtract, multiply, and divide fractions, along with a helpful worksheet to practice your skills.
Understanding Fractions

Before diving into the operations, it’s essential to understand the basics of fractions. A fraction represents a part of a whole and consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into.
Adding Fractions

Adding fractions is a straightforward process, but it requires a common denominator. Here are the steps:
- Check if the denominators are the same. If they are, you can add the numerators directly.
- If the denominators are different, find the least common multiple (LCM) of the two denominators.
- Convert both fractions to have the LCM as the denominator.
- Add the numerators.
Example:
Add 1⁄4 and 1⁄6
- The denominators are different, so we need to find the LCM of 4 and 6, which is 12.
- Convert both fractions: 1⁄4 = 3⁄12 and 1⁄6 = 2⁄12
- Add the numerators: 3 + 2 = 5
- The answer is 5⁄12
Subtracting Fractions
Subtracting fractions follows the same steps as adding fractions, with one slight difference:
- Check if the denominators are the same. If they are, you can subtract the numerators directly.
- If the denominators are different, find the least common multiple (LCM) of the two denominators.
- Convert both fractions to have the LCM as the denominator.
- Subtract the numerators.
Example:
Subtract 1⁄4 from 1⁄6
- The denominators are different, so we need to find the LCM of 4 and 6, which is 12.
- Convert both fractions: 1⁄4 = 3⁄12 and 1⁄6 = 2⁄12
- Subtract the numerators: 3 - 2 = 1
- The answer is 1⁄12
Multiplying Fractions

Multiplying fractions is a bit different from adding and subtracting. Here are the steps:
- Multiply the numerators.
- Multiply the denominators.
- Simplify the result, if possible.
Example:
Multiply 1⁄2 and 3⁄4
- Multiply the numerators: 1 × 3 = 3
- Multiply the denominators: 2 × 4 = 8
- The answer is 3⁄8
Dividing Fractions

Dividing fractions involves inverting the second fraction and multiplying. Here are the steps:
- Invert the second fraction (i.e., flip the numerator and denominator).
- Multiply the fractions.
- Simplify the result, if possible.
Example:
Divide 1⁄2 by 3⁄4
- Invert the second fraction: 3⁄4 becomes 4⁄3
- Multiply the fractions: 1⁄2 × 4⁄3 = 4⁄6
- Simplify the result: 4⁄6 = 2⁄3
Fractions Worksheet

Now that you’ve learned the basics of adding, subtracting, multiplying, and dividing fractions, it’s time to practice! Here’s a helpful worksheet to get you started:
| Operation | Problem | Answer |
|---|---|---|
| Addition | 1/4 + 1/6 | _____ |
| Subtraction | 1/4 - 1/6 | _____ |
| Multiplication | 1/2 × 3/4 | _____ |
| Division | 1/2 ÷ 3/4 | _____ |
| Addition | 2/3 + 1/5 | _____ |
| Subtraction | 2/3 - 1/5 | _____ |
| Multiplication | 2/3 × 1/5 | _____ |
| Division | 2/3 ÷ 1/5 | _____ |

Fill in the answers to the problems and check your work!
📝 Note: Make sure to simplify your answers whenever possible.
By practicing with this worksheet, you’ll become more confident in your ability to add, subtract, multiply, and divide fractions. Remember to take your time and follow the steps outlined above. Happy practicing!
What is the least common multiple (LCM)?

+
The least common multiple (LCM) is the smallest number that is a multiple of two or more numbers.
How do I simplify a fraction?

+
To simplify a fraction, divide the numerator and denominator by the greatest common divisor (GCD).
Can I add or subtract fractions with different denominators?
+
Yes, but you need to find the least common multiple (LCM) of the denominators first.