Mastering Fractions: Your Ultimate Addition Worksheet Guide

Embarking on the journey of understanding fractions can be both exciting and intimidating for many students. As a fundamental aspect of mathematics, fractions not only prepare you for advanced math but also find applications in everyday life—from cooking to carpentry. This guide will walk you through the process of adding fractions using worksheets, ensuring you have the tools needed to master this skill with confidence.
Why are Fractions Important?

Fractions help in several key areas:
- Numeracy Skills: Grasping how fractions work is crucial for basic arithmetic and advancing to more complex mathematical concepts.
- Real-world Applications: They are essential in tasks like measuring ingredients, scaling distances, and dividing resources.
- Problem Solving: Fractions foster a deeper understanding of ratios and proportions, which are vital for logical thinking and problem-solving.
The Basics of Adding Fractions

Before diving into worksheets, here are some fundamental principles:
- Only fractions with the same denominator (bottom number) can be added directly.
- Fractions with different denominators must be converted to have a common denominator before addition.
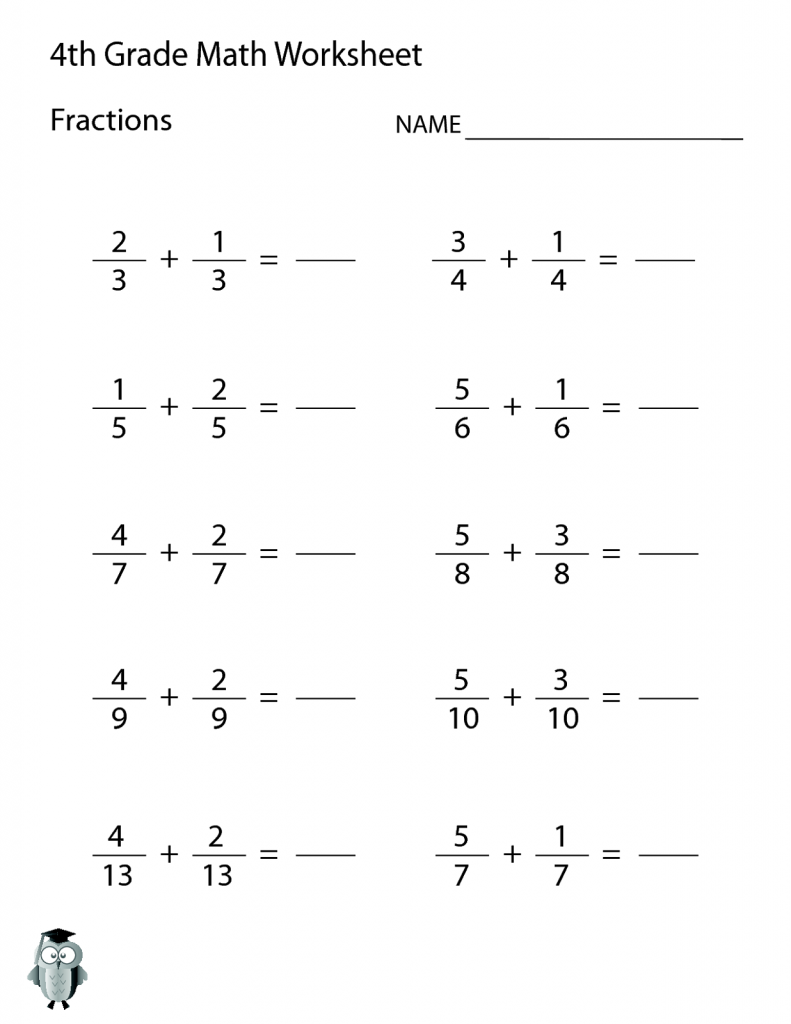
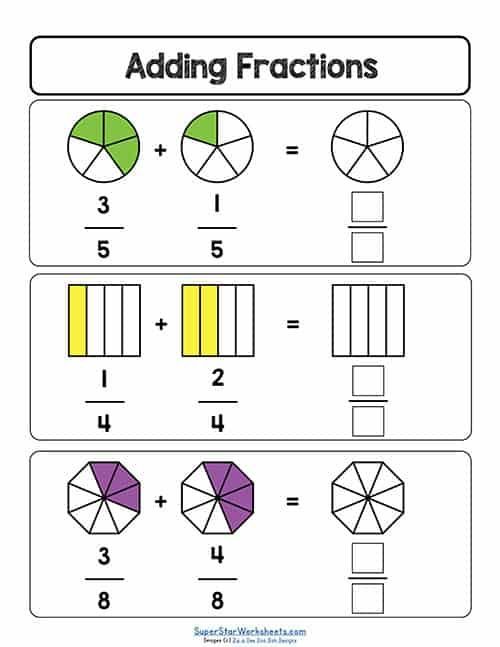
Fraction Addition with Like Denominators

When adding fractions with like denominators:
- Keep the denominator constant.
- Add the numerators (top numbers).
- Simplify the result if possible.
Here’s an example:
| Fraction 1 | Fraction 2 | Result |
|---|---|---|
| 3⁄5 | 1⁄5 | 4⁄5 |
Fraction Addition with Unlike Denominators

When denominators differ, follow these steps:
- Identify the least common denominator (LCD).
- Convert each fraction to have the LCD as its denominator by multiplying both the numerator and the denominator by the same value.
- Add the numerators.
- Reduce the fraction to its simplest form.
Example:
| Fraction 1 | Fraction 2 | LCD | Converted | Result |
|---|---|---|---|---|
| 1⁄2 | 1⁄3 | 6 | 3⁄6 and 2⁄6 | 5⁄6 |
📝 Note: Remember to always simplify your final answer to its lowest terms to avoid overcomplicating calculations.
Worksheet Strategies

Designing Your Fraction Addition Worksheet

When creating or choosing worksheets:
- Begin with simple fractions to build confidence.
- Introduce mixed numbers and improper fractions gradually.
- Incorporate word problems for real-life context.
- Include exercises for finding the LCD.
Using Worksheets to Learn Fraction Addition

Here are some strategies for effectively using fraction worksheets:
- Use color-coding or visual aids to identify the parts of fractions.
- Encourage students to explain their solutions to foster understanding.
- Provide examples followed by similar practice problems to solidify concepts.
Practice Makes Perfect

Regular practice is key. Here are ways to maximize your learning:
- Set aside time each day for fraction practice.
- Use varied worksheets to challenge different aspects of fraction addition.
- Encourage self-assessment by allowing students to create their own problems.
🔍 Note: Regular self-assessment helps students identify areas for improvement, making practice more effective.
Understanding how to add fractions and utilizing worksheets effectively is not just about mastering a mathematical concept; it's about opening the door to a world of numbers that govern our daily lives. From dividing a recipe in half to understanding financial ratios, fractions are everywhere. By following this guide, you'll be well on your way to not only improving your numeracy but also your ability to make sense of the world through numbers.
Why do we need to find the least common denominator?
+
Finding the least common denominator allows you to add fractions with different denominators by giving them a common base, ensuring accurate addition.
How can I practice adding fractions?

+
You can practice adding fractions through regular use of fraction addition worksheets, flashcards, or interactive online tools that offer instant feedback.
What are common mistakes when adding fractions?

+
Common errors include adding numerators and denominators separately, not finding the LCD, or forgetting to simplify the result.