Mastering Fraction Addition: Unlike Denominators Worksheet
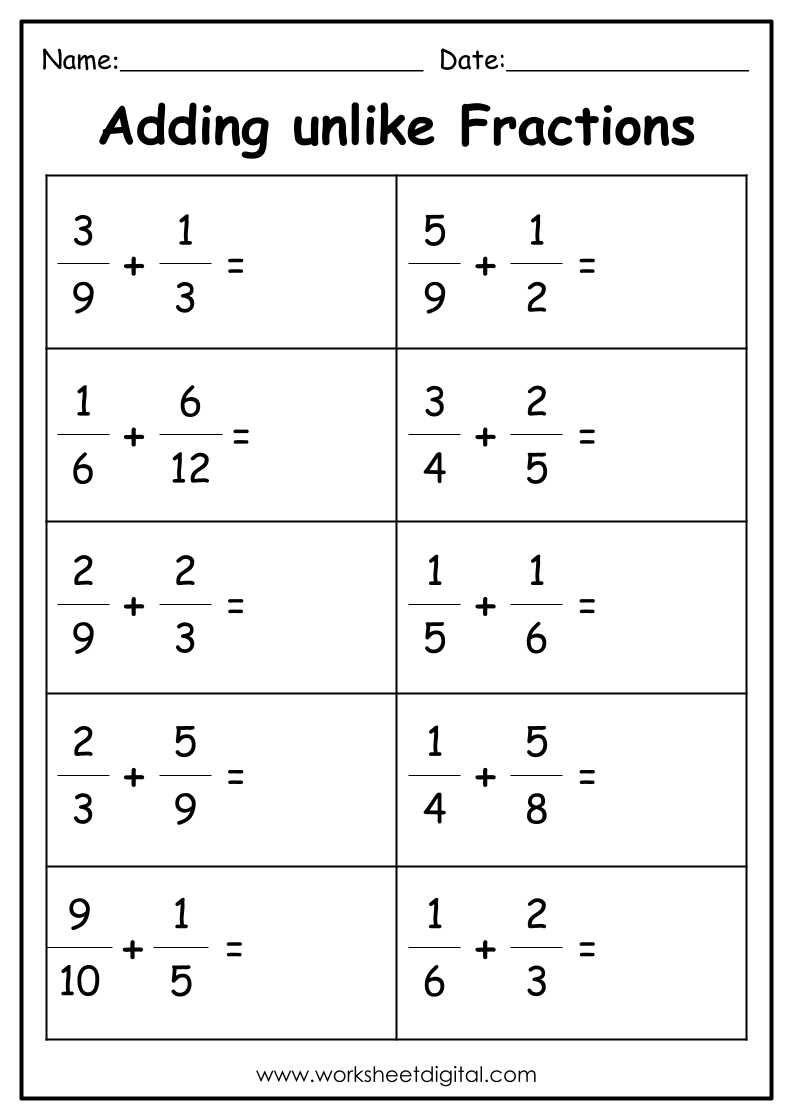
Fractions can often appear daunting, especially when it comes to adding unlike denominators. Unlike denominators mean the denominators of the fractions you wish to add are not the same. This can complicate the process, but with the right approach, you can master this fundamental arithmetic operation effortlessly.
Understanding Unlike Denominators

To add fractions with unlike denominators, the first step is understanding why having different denominators poses a challenge:
- Denominator Meaning: The denominator of a fraction indicates the number of equal parts a whole is divided into. Unlike denominators mean the fractions are divided differently.
- Equivalence: To add fractions, they need to have a common denominator. This creates equivalence, making the operation valid.
Steps to Add Fractions with Unlike Denominators
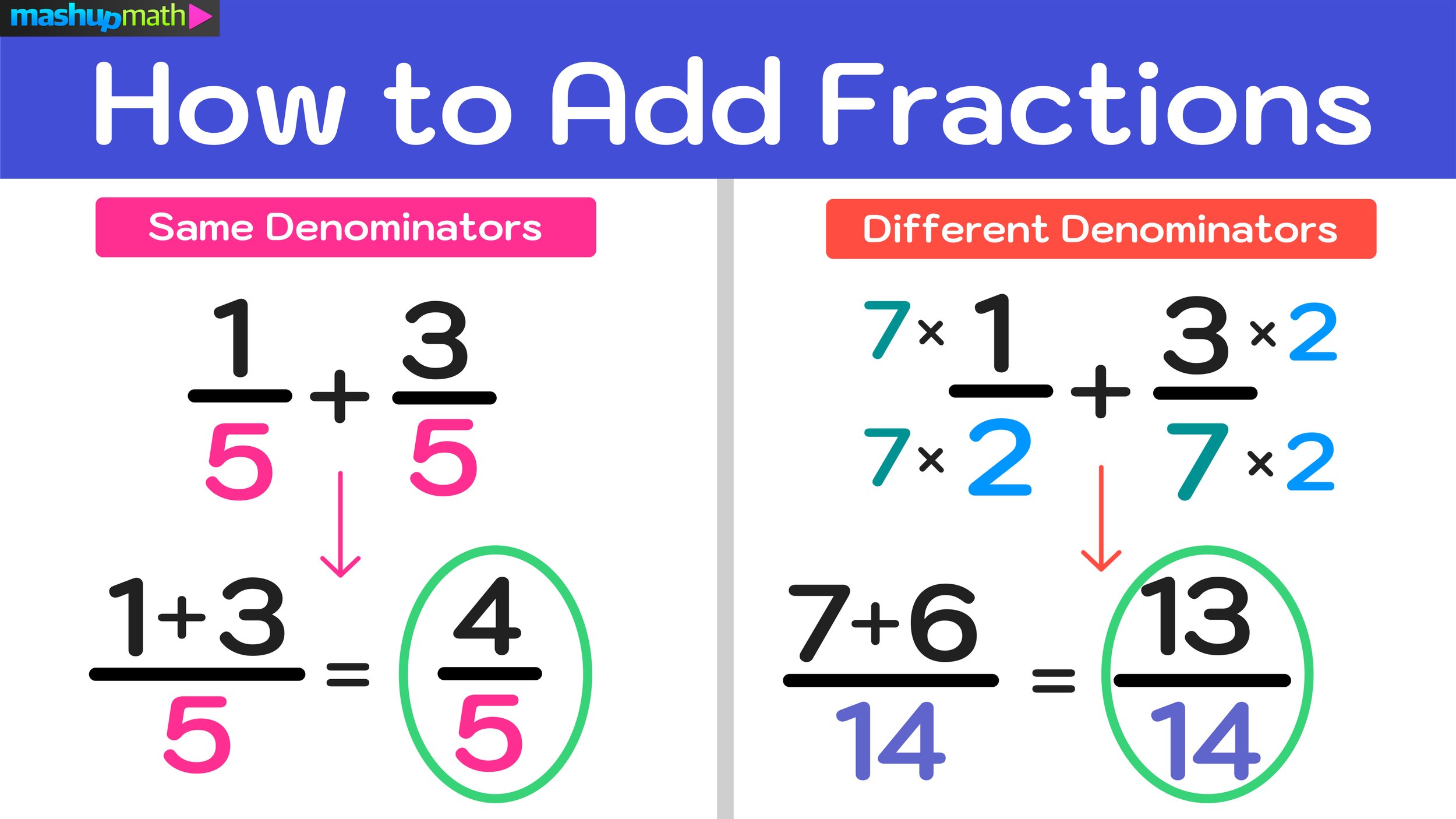
Finding the Least Common Denominator (LCD)

The least common denominator (LCD) is the smallest (or least) common multiple of the given denominators. Here’s how you find it:
- List the multiples of each denominator.
- Identify the smallest multiple that appears in all lists.
For instance, if you’re adding 1⁄4 and 1⁄6:
| Denominator | Multiples |
|---|---|
| 4 | 4, 8, 12, 16, 20… |
| 6 | 6, 12, 18, 24… |

The least common multiple of 4 and 6 is 12. Thus, the LCD is 12.
Converting to the LCD

Now, convert each fraction to an equivalent fraction with the LCD:
- 1⁄4 becomes (1⁄4) * (3⁄3) = 3⁄12
- 1⁄6 becomes (1⁄6) * (2⁄2) = 2⁄12
Adding the Fractions

After converting both fractions to their equivalent forms with the same denominator, simply add the numerators:
3⁄12 + 2⁄12 = 5⁄12
Practice with Worksheets

Here are some steps to create or use a worksheet for unlike denominator addition:
- Define the scope: Decide on the range of denominators you’ll practice with.
- Create problems: Generate problems with varying denominators. Ensure some problems include mixed numbers as well.
- Work on solutions: Solve these problems in one section of the worksheet, following the steps outlined above.
📝 Note: Creating your worksheet allows for personalized practice, targeting exactly where you need improvement.
Key Concepts to Remember
- Prime factorization: Breaking down numbers into their prime factors can simplify finding the LCD.
- Equivalent fractions: Always convert fractions to have the same denominator before adding.
- Reducing fractions: After adding, check if the fraction can be reduced to its simplest form.
Mastering the art of adding fractions with unlike denominators requires understanding and practice. By following these steps, you'll not only improve your fraction arithmetic skills but also gain confidence in handling more complex math operations. Remember, mathematics is not just about the numbers but about understanding and applying concepts logically.
Why do we need to find the LCD?

+
Adding fractions requires the parts you’re adding to be of the same size (the denominator). The least common denominator (LCD) ensures that all fractions being added are in terms of equal parts.
Can’t I just multiply the denominators to find the LCD?

+
While you could do this, it would often result in a much larger denominator than necessary, making the problem more complex than it needs to be. The LCD is the smallest possible common denominator for efficient addition.
How can I improve my speed in finding LCDs?

+
Practice with prime factorization. Knowing your prime numbers and being able to quickly factorize larger numbers will help you identify the LCD faster.