5 Ways to Master Adding and Subtracting Unlike Denominators
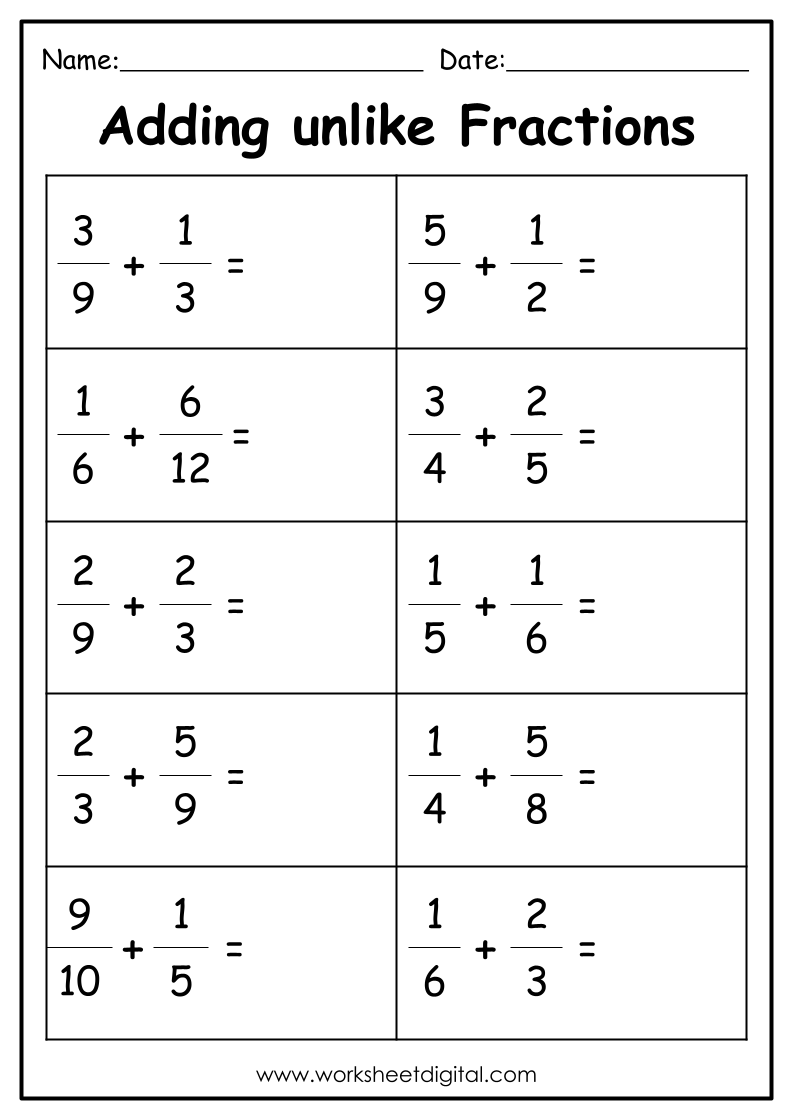
In the journey to master mathematics, one of the foundational skills that often gives students pause is the manipulation of fractions, particularly when the denominators are different. Adding and subtracting unlike denominators is a key skill for everyday applications, as well as a crucial step towards understanding more complex mathematical operations. This blog post will guide you through 5 ways to confidently navigate these arithmetic waters, transforming what may seem like a daunting task into a straightforward exercise in number sense.
Understanding the Basics of Fractions

Before diving into the manipulation, understanding fractions is key:
- Numerator: The top number representing the part of the whole or the quantity.
- Denominator: The bottom number signifying how many parts the whole is divided into.
Having a solid grasp of these concepts sets the stage for adding and subtracting unlike denominators with greater ease.
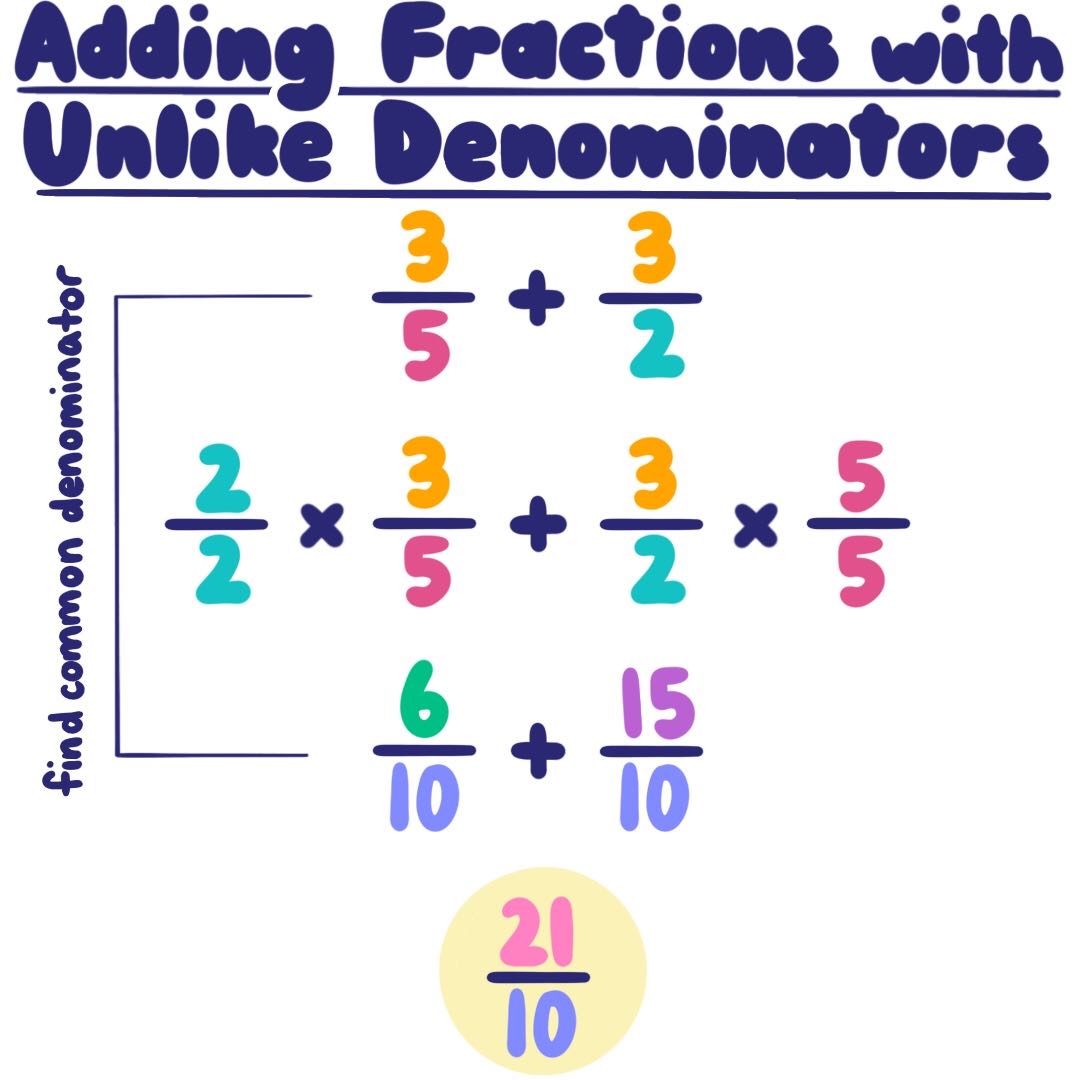
Method 1: Finding a Common Denominator

The cornerstone of adding and subtracting fractions with unlike denominators is to find a common ground or, more precisely, a common denominator. Here’s how you can do it:
- Identify the Least Common Multiple (LCM): List multiples of both denominators until you find the smallest shared number.
- Convert Fractions: Adjust each fraction to have the LCM as their new denominator, preserving their value by multiplying both the numerator and the denominator by the same factor.
- Add or Subtract: Once the denominators are the same, add or subtract the numerators as usual.

🔎 Note: Finding the LCM manually can be cumbersome for larger numbers. Use tools or apply prime factorization for efficiency.
Method 2: Using the Butterfly Method

This visual method aids in finding a common denominator effortlessly:
- Multiply the denominators to find the new denominator.
- Cross-multiply to determine the new numerators.
- Add or subtract the cross-products to get the new numerator.

The Butterfly method isn’t just fun; it’s also an intuitive way to tackle unlike denominators, especially for younger learners or those new to the subject.
Method 3: Prime Factorization

Prime factorization simplifies finding a common denominator:
- Factorize both denominators into prime factors.
- Multiply each factor to its highest power to form the LCM.
- Convert each fraction using this LCM.
| Denominator 1 | Denominator 2 | LCM |
|---|---|---|
| 4 = 22 | 6 = 2 * 3 | 12 = 22 * 3 |
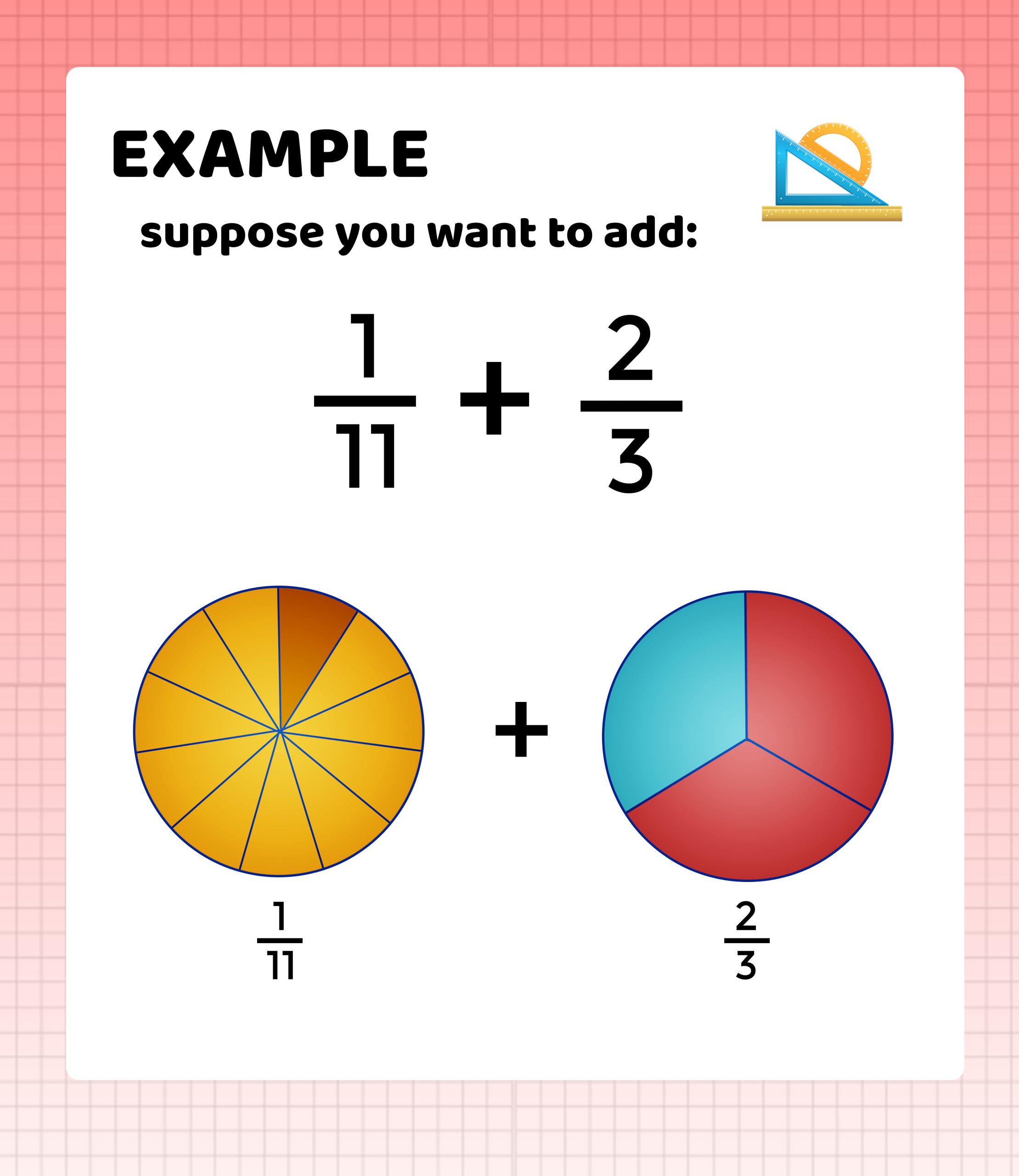
🔧 Note: This method is most beneficial for larger numbers where LCM isn’t easily identifiable at a glance.
Method 4: Adding Mixed Numbers

Mixed numbers require an additional step:
- Convert mixed numbers to improper fractions.
- Find the LCM of the denominators.
- Add or subtract as with simple fractions.
- Convert the result back to a mixed number if necessary.
🔗 Note: Remember to simplify the result, reducing the fraction to its lowest terms.
Method 5: Practice with Different Scenarios
Mastery in adding and subtracting unlike denominators comes with consistent practice:
- Drills with different types of fractions.
- Real-life word problems.
- Using online tools or software designed for this purpose.
These five methods offer a roadmap to confidently manage unlike denominators. Whether you are a student, a teacher, or someone simply brushing up on math skills, these strategies provide multiple pathways to understanding and proficiency. Remember, each person learns differently, so experimenting with these methods can help identify which one resonates best with your learning style or teaching approach.
What is the best method for teaching unlike denominators?

+
The best method often depends on the learner’s preference. However, combining visual aids like the Butterfly method with number drills can provide a comprehensive understanding.
How can I help a student who struggles with finding the LCM?

+
Introduce the concept using real-life examples, like finding a common time for two events or a common meeting point. Also, using prime factorization can simplify the process for students struggling with larger numbers.
Why are unlike denominators important?
+
Understanding how to work with unlike denominators is fundamental in algebra and beyond. It’s key for simplifying expressions, solving equations, and calculating proportions and ratios in real-world scenarios.