Adding and Subtracting Fractions with Ease: Worksheet Guide
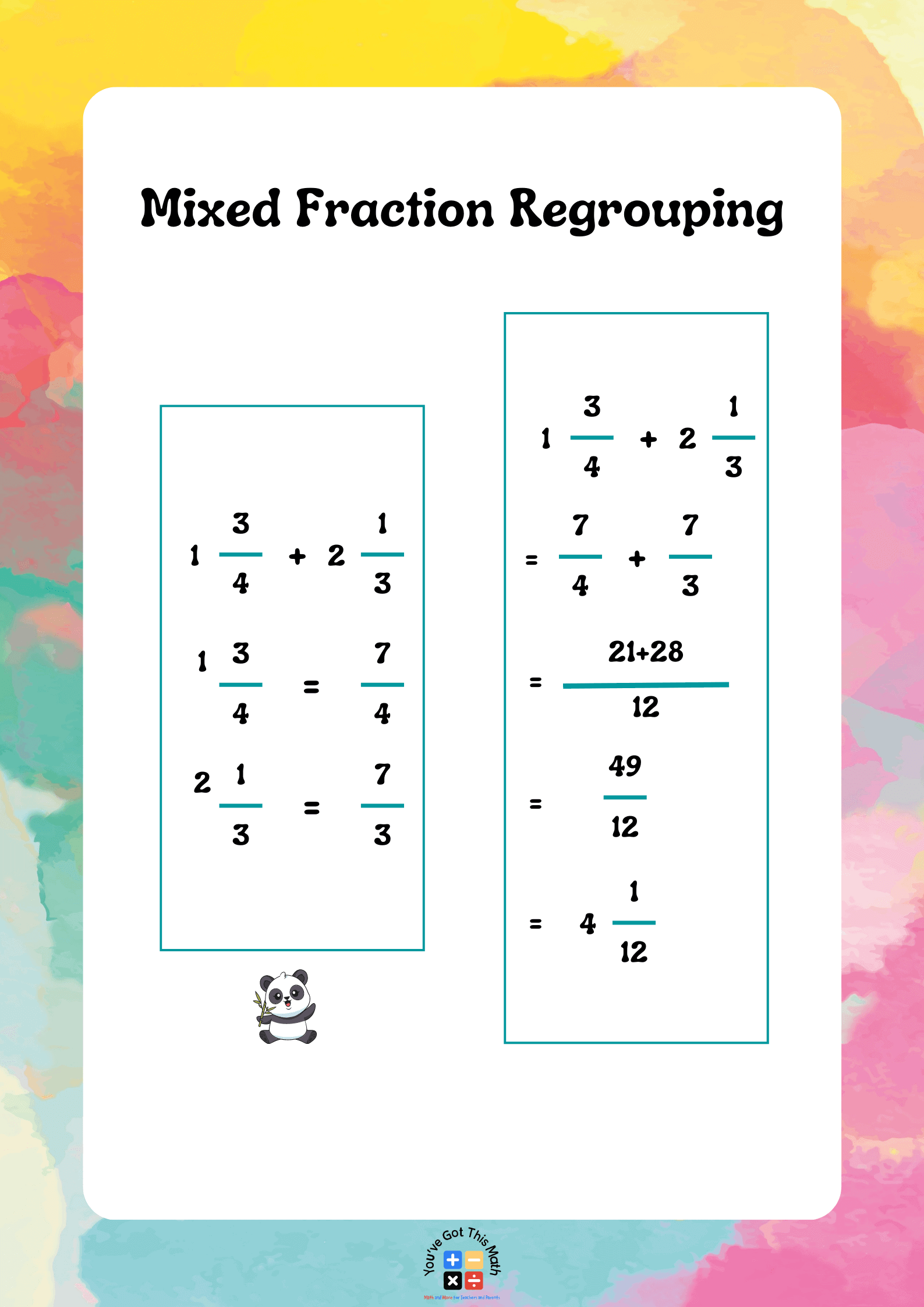
🌟 Note: This post focuses on simplifying the process of adding and subtracting fractions for elementary to middle school students and their guardians, offering a structured guide for those encountering these math concepts.
Understanding the Basics

Before diving into the actual process of adding and subtracting fractions, let’s grasp the fundamentals.
Fractions are a representation of a part of a whole. Here’s what you need to know:
- Numerator: The top number in a fraction that indicates the number of parts you have.
- Denominator: The bottom number which represents how many equal parts the whole is divided into.
- When adding or subtracting fractions, the key is to ensure the denominators are the same to avoid confusion.
💡 Note: The value of a fraction is determined by the relationship between the numerator and the denominator, not just their individual values.
Steps to Add or Subtract Fractions

The following steps will guide you through the process:
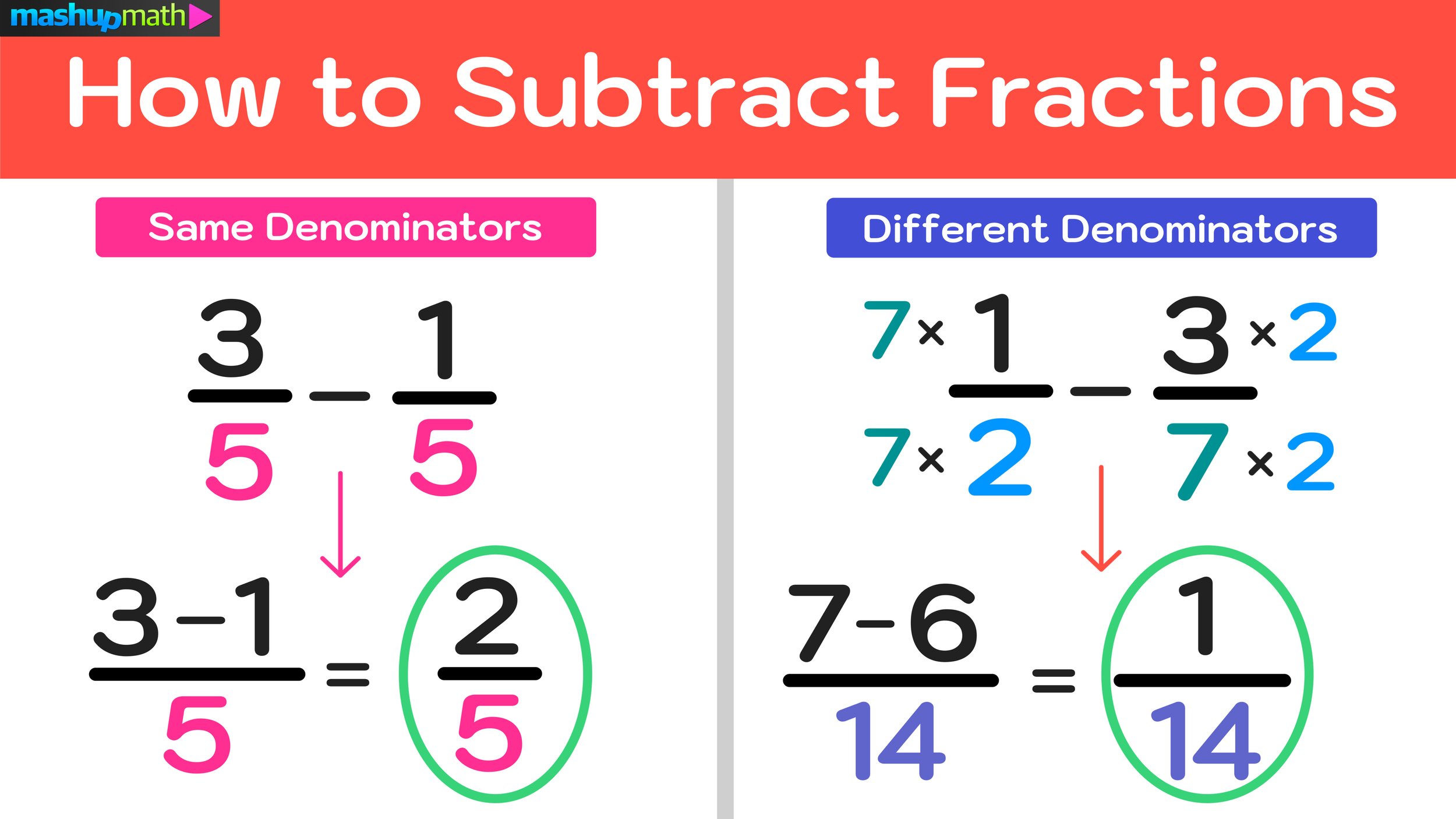
Step 1: Check the Denominators

If the denominators are identical:
- Directly add or subtract the numerators.
- Keep the common denominator in the result.
If the denominators differ, you need to:
- Find the Least Common Denominator (LCD).
- Convert both fractions to have this common denominator.
Here’s a table to illustrate:
| Scenario | Example |
|---|---|
| Same Denominator | 1/4 + 3/4 = (1 + 3)/4 = 4/4 |
| Different Denominators | 1/2 + 1/3 = (3/6) + (2/6) = 5/6 |

Step 2: Convert to the Common Denominator

If you need to convert:
- Multiply the numerator and denominator of each fraction by the same value to reach the LCD.
- Perform the addition or subtraction as described in Step 1.
⚠️ Note: When converting fractions, always ensure both the numerator and the denominator are multiplied by the same number to maintain the fraction's value.
Step 3: Simplify the Result

The final result might be an improper fraction, in which case:
- Convert it to a mixed number if necessary.
- Reduce the fraction to its simplest form by dividing both the numerator and the denominator by their Greatest Common Divisor (GCD).
Practical Examples
Let’s put these steps into practice:
- Addition with Same Denominators: 5/8 + 3/8 = 8/8 = 1 (or 1 0/8 simplified)
- Subtraction with Different Denominators: 3/4 - 1/6 = (9/12) - (2/12) = 7/12
- Adding Mixed Numbers: 1 3/4 + 2 1/2 = (1 6/8) + (2 4/8) = 3 10/8 = 3 1/4
Common Mistakes and How to Avoid Them

Here are some common mistakes and how to avoid them:
- Mismatching Denominators: Always make sure fractions have the same denominator before performing operations.
- Over-Simplifying: Don't simplify intermediate steps until the final calculation.
- Incorrect Multiplication: When converting, multiply both the numerator and the denominator by the same number.
🔍 Note: Regular practice with different scenarios can help in recognizing these mistakes and improving accuracy.
Final Thoughts

Understanding how to add and subtract fractions is a crucial step in mastering basic arithmetic. By following the steps outlined, you’ll be able to tackle various problems confidently. Remember to:
- Always check for common denominators.
- Convert fractions when necessary.
- Reduce the final answer to its simplest form.
Mastering these skills opens the door to more complex mathematics, making it easier to handle mathematical equations and real-life situations involving fractions.
Wrapping Up

Adding and subtracting fractions is a skill that, once learned, serves as a foundation for a wide array of mathematical tasks. With practice and the right guidance, it becomes straightforward. Keep practicing, and these operations will become second nature.
Why do we need a common denominator when adding or subtracting fractions?

+
A common denominator is needed to ensure that you are working with fractions that represent the same whole, making the addition or subtraction meaningful.
What if one fraction is positive and the other negative?

+
Subtract the smaller fraction from the larger one as if both were positive, then place the sign of the fraction with the larger absolute value.
How do I know when to convert fractions to mixed numbers?

+
Convert to a mixed number if the result is an improper fraction where the numerator is larger than the denominator to make the value more tangible.