5 Simple Steps to Master Fraction Calculations

Understanding fractions is crucial for daily mathematics, from cooking to solving complex problems in algebra. While they might seem daunting at first, with the right approach, mastering fraction calculations can be made simple and fun. Here are five straightforward steps to help you conquer the world of fractions:
Understanding Fraction Basics
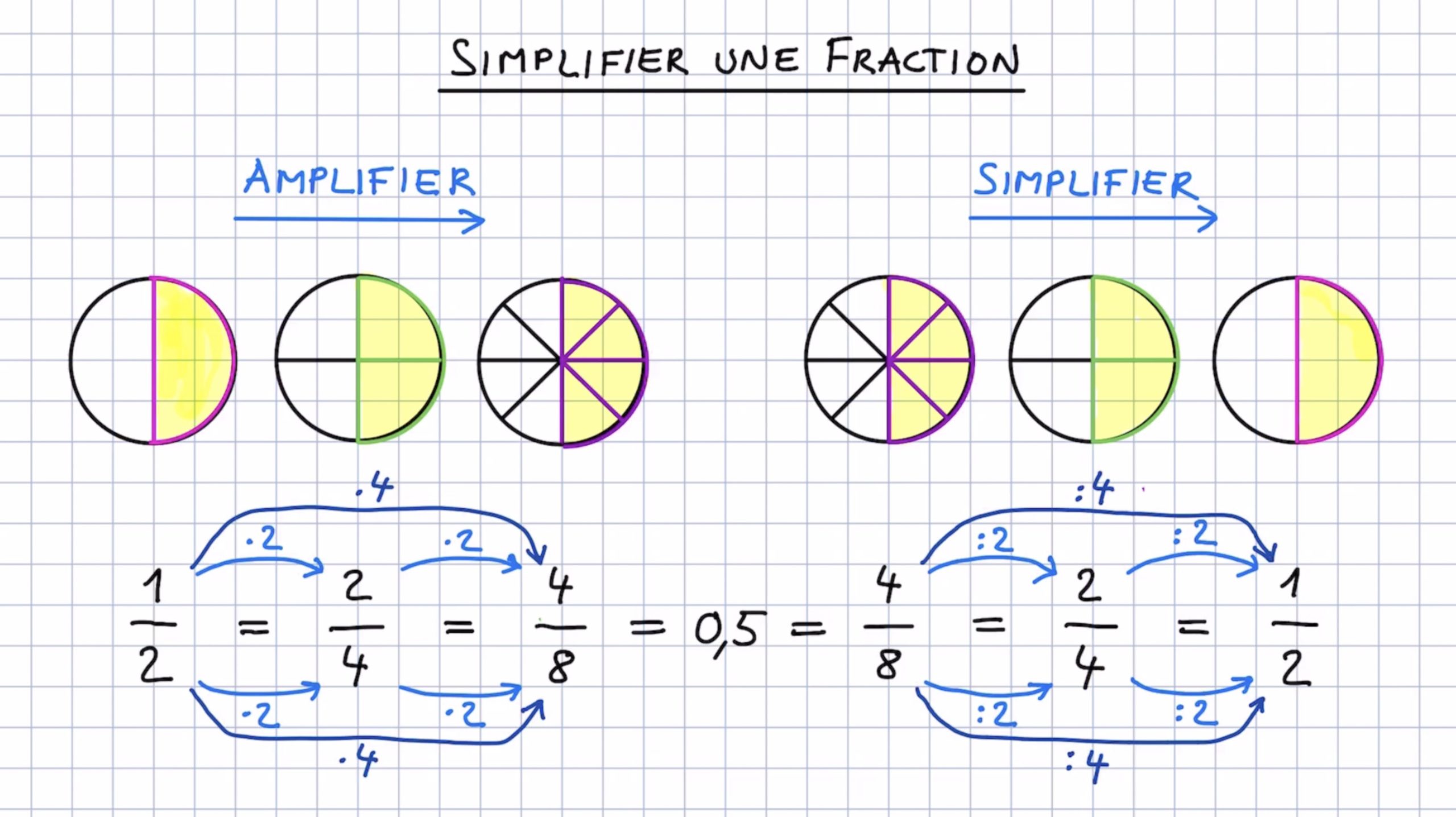

Before diving into calculations, grasp the fundamental concept of a fraction:
- Numerator: The top number indicating the portion of the whole.
- Denominator: The bottom number showing the total parts the whole is divided into.
📚 Note: Remember, a fraction like 2/4 can be simplified to 1/2, where the numerator and denominator share common factors.
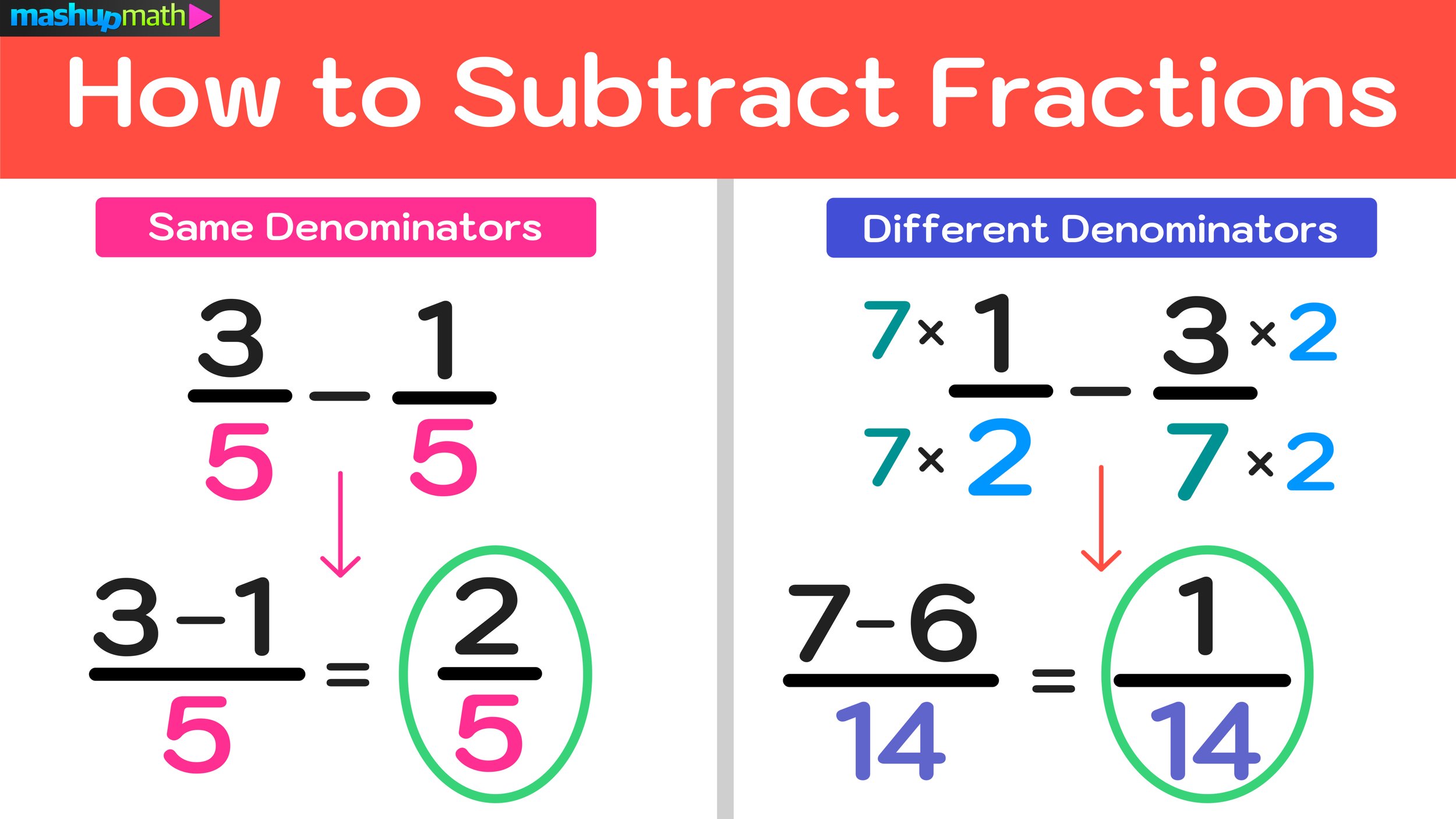
Adding and Subtracting Fractions


Here’s how to approach these operations:
- Common Denominator: Find a common denominator for the fractions you’re adding or subtracting.
- Convert: Convert all fractions to have the same denominator.
- Operate: Add or subtract the numerators, keeping the denominator the same.
- Simplify: Reduce the resulting fraction to its simplest form if possible.
🎲 Note: If you need to add or subtract more complex fractions, using the least common multiple as the denominator can be a time-saver.
Multiplying and Dividing Fractions

To multiply or divide fractions:
- Multiplying: Multiply the numerators together and the denominators together. Simplify afterward if possible.
- Dividing: Flip the second fraction (take the reciprocal), then multiply.
Here's a practical example:
| Operation | Example |
|---|---|
| Multiplication | \frac{3}{4} \times \frac{2}{5} = \frac{3 \times 2}{4 \times 5} = \frac{6}{20} = \frac{3}{10} |
| Division | \frac{3}{4} \div \frac{2}{5} = \frac{3}{4} \times \frac{5}{2} = \frac{3 \times 5}{4 \times 2} = \frac{15}{8} = 1 \frac{7}{8} |

🧮 Note: While multiplying fractions is straightforward, division can be easily understood by thinking of it as multiplying by the reciprocal.
Converting Between Mixed Numbers and Improper Fractions


Knowing how to switch between these formats is essential:
- From Mixed Number to Improper Fraction: Multiply the whole number by the denominator of the fraction, add the numerator, then place over the same denominator.
- From Improper Fraction to Mixed Number: Divide the numerator by the denominator to find the whole number part, the remainder becomes the numerator over the original denominator.
Applying Fraction Operations to Real-Life Problems

Here’s where fractions come alive:
- Recipes: Adjust ingredient amounts when you need to double or halve a recipe.
- Measurements: Convert measurements to work with fractions; think of converting inches to fractions of feet.
- Time: Work with time management, where fractions help divide a task into smaller, manageable units.
By mastering these steps, you'll gain the confidence to tackle any fraction problem. Whether you're adjusting a recipe to cater to a small or large group or calculating a project's completion time, fractions are your friends. Your mathematical journey has just begun, with a firm foundation in fraction calculations to explore further complex mathematics.
Why are fractions important in everyday life?

+
Fractions are fundamental for numerous real-world applications like cooking, carpentry, financial calculations, and even understanding time management.
How can I simplify fractions?

+
To simplify, find the greatest common divisor (GCD) of both the numerator and the denominator, then divide both by this number.
What’s the difference between multiplying and dividing fractions?

+
When multiplying, you multiply numerators together and denominators together. For division, you flip the second fraction and then multiply.