Simplify Rational Expressions: Add & Subtract Worksheet

Working with rational expressions, akin to managing fractions, can be a daunting yet rewarding task in algebra. These expressions play a crucial role in simplifying mathematical problems across various scientific and engineering fields. Adding and subtracting rational expressions requires a methodical approach to arrive at a simplified form. This comprehensive guide will walk you through the step-by-step process of simplifying these expressions, ensuring that you not only understand but also master this important algebraic concept.

Understanding Rational Expressions

Before delving into simplification, it's essential to grasp what rational expressions are. A rational expression is essentially a fraction where the numerator and/or the denominator are polynomials. Here's a simple example:

This example shows a polynomial (x^2 + 3x + 2) over another polynomial (x^2 - x - 2). Now, let's explore how to add and subtract these expressions.

Step-by-Step Guide to Simplifying Rational Expressions

1. Find a Common Denominator: Much like adding fractions, the first step is to find a common denominator. If the denominators are already the same, you can proceed to add or subtract the numerators directly. If not:
• If the denominators differ, find their Least Common Multiple (LCM). Here's an example:

  Denominators	Prime Factorization
  x^2 - 4	(x - 2)(x + 2)
  x - 2	x - 2

  
  
  Here, the LCM would be (x - 2)(x + 2)(x - 2) or x^2 - 4.
2. Adjust Expressions for Common Denominator: Once you have a common denominator, adjust each rational expression by multiplying both the numerator and the denominator by the missing factor(s) to make the denominators match.
3. Add or Subtract the Numerators: With the common denominator in place, add or subtract the numerators as needed. Remember, you're not adding or subtracting the denominators; they remain the same.
4. Simplify the Resulting Expression: Finally, simplify your resulting expression by factoring, canceling common factors, and reducing to the simplest form where possible.

⚠️ Note: Always check for any restrictions where your rational expression is undefined, such as where the denominator equals zero.

Examples of Adding and Subtracting Rational Expressions

Let's illustrate the process with some examples:

Example 1: Adding with Different Denominators

• Find the LCM: The first denominator is already in factored form, x(x + 1), and the second denominator is x + 1, so the LCM is x(x + 1)(x + 1) = x(x + 1)^2.
• Adjust the expressions:
  • (2x - 3)(x + 1) / x(x + 1)^2
  • 5x / x(x + 1)^2
• Add the numerators: (2x^2 + x - 3 + 5x) / x(x + 1)^2 = (2x^2 + 6x - 3) / x(x + 1)^2
• Simplify: This is already in its simplest form.

Example 2: Subtracting with a Common Denominator

• Since the denominators are already the same, subtract the numerators: (x + 2 - 3x + 1) / (x - 1) = (-2x + 3) / (x - 1)
• Simplify: Factor the numerator if possible; in this case, it's already simplified.

🔎 Note: When simplifying, always look for common factors between numerator and denominator to simplify further.

Wrapping Up

Handling rational expressions in addition and subtraction necessitates an understanding of factorization, finding the least common multiple, and applying the principles of fraction arithmetic. By following the steps outlined above, you can demystify the process of simplifying these expressions. Remember that rational expressions are found in many practical applications, from solving complex engineering problems to analyzing financial equations. Therefore, mastering this skill not only strengthens your algebraic prowess but also prepares you for real-world problem-solving scenarios.

Through practice, these steps will become second nature, enabling you to navigate through algebraic challenges with ease and precision.

What if there’s no common denominator?

+

If the denominators do not have a common factor, multiply the numerators by the other denominators and combine them into one expression over the product of the original denominators.

How do I simplify the final expression?

+

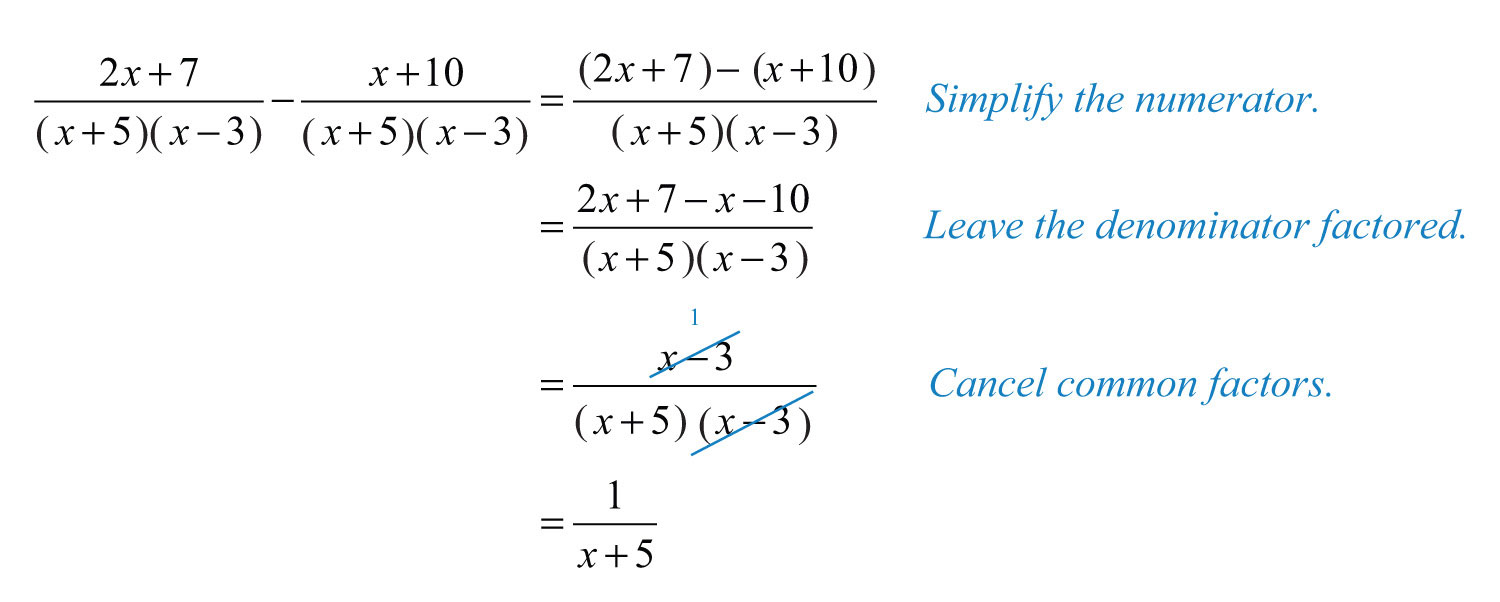
After adding or subtracting, factor the numerator and denominator, then cancel out common factors. This reduces the expression to its simplest form.

Can the denominator be zero?

+

No, the denominator of a rational expression cannot be zero. Any value of x that makes the denominator zero should be noted as making the expression undefined.