Absolute Value Worksheet: Master the Basics with Ease

In the world of mathematics, understanding the concept of absolute value is crucial as it represents the non-negative value of a number irrespective of its sign. Often encountered in algebraic expressions, geometric distances, and calculus, mastering absolute value can significantly enhance your problem-solving skills. This comprehensive guide delves into the basics, rules, and practical applications of absolute value, equipping you with worksheets and tips to grasp this fundamental concept with ease.
What is Absolute Value?

The absolute value of a number is its distance from zero on the number line. Represented by two vertical bars surrounding the number, like |x|, absolute value provides the positive magnitude of any real number. Here are some key points to remember:
- The absolute value of a positive number or zero is the number itself: |x| = x for x ≥ 0.
- For negative numbers, the absolute value is the positive counterpart: |x| = -x for x < 0.
- Essentially, absolute value turns negative numbers into positive, leaving zeros and positives unchanged.
Basic Rules of Absolute Value

Before diving into problem-solving, here are some fundamental rules that govern absolute value:
- Non-negativity: |x| ≥ 0 for all x ∈ R.
- Equality: |x| = 0 if and only if x = 0.
- Addition and Subtraction: |x + y| ≤ |x| + |y| and |x - y| ≥ ||x| - |y||.
- Multiplication: |x · y| = |x| · |y|.
- Division: |x ÷ y| = |x| ÷ |y| for y ≠ 0.
These rules provide the groundwork for simplifying absolute value expressions.
Worksheet for Mastering Absolute Value

To solidify your understanding, here is a simple worksheet to practice absolute value calculations:
| Expression | Answer |
|---|---|
| |12| | 12 |
| |-7| | 7 |
| |0| | 0 |
| |4 - 8| | 4 |
| |5| - |9| | 4 |
| |-3.5| | 3.5 |
| |7 + (-10)| | 3 |
| |3/4| | 3/4 |

Completing this worksheet will help you understand how absolute value operates in different scenarios.
Applying Absolute Value in Real-Life

Let’s look at some practical applications where absolute value comes into play:
- Temperature Differences: Absolute value can measure the difference between two temperatures irrespective of whether it’s increasing or decreasing.
- Distance: When calculating the distance between two points on the number line or in a coordinate system, absolute value helps by considering the positive distance.
- Electronics: In electrical engineering, the magnitude of voltage or current is often described using absolute values.
- Finance: Absolute value can help determine the percentage change in stock prices or the magnitude of financial losses/gains.
Tips for Solving Absolute Value Equations

Here are some strategies for tackling equations involving absolute values:
- Consider Both Cases: When solving |x| = a, you must solve for both x = a and x = -a.
- Remove Absolute Value: To eliminate the absolute value sign, set up two equations based on whether the expression inside the absolute value is positive or negative.
- Graphical Method: On a number line or graph, draw points at ±a, where a is the value inside the absolute value, and extend lines from these points to find the solution region.
📝 Note: Remember to double-check your solutions in absolute value equations. Sometimes, only one solution will be valid based on the original conditions.
Understanding and working with absolute value is more than just about performing mathematical operations; it's about recognizing its practical applications and mastering the nuances of its rules. Whether you're preparing for an exam or simply expanding your mathematical knowledge, this exploration into absolute value will serve as a robust foundation for further mathematical endeavors. The key takeaway is to always consider the distance from zero and understand how this fundamental concept impacts various fields beyond pure mathematics.
What does the absolute value of a number indicate?

+
The absolute value of a number represents its distance from zero on the number line, essentially providing its magnitude without regard to its sign.
Can absolute value be negative?
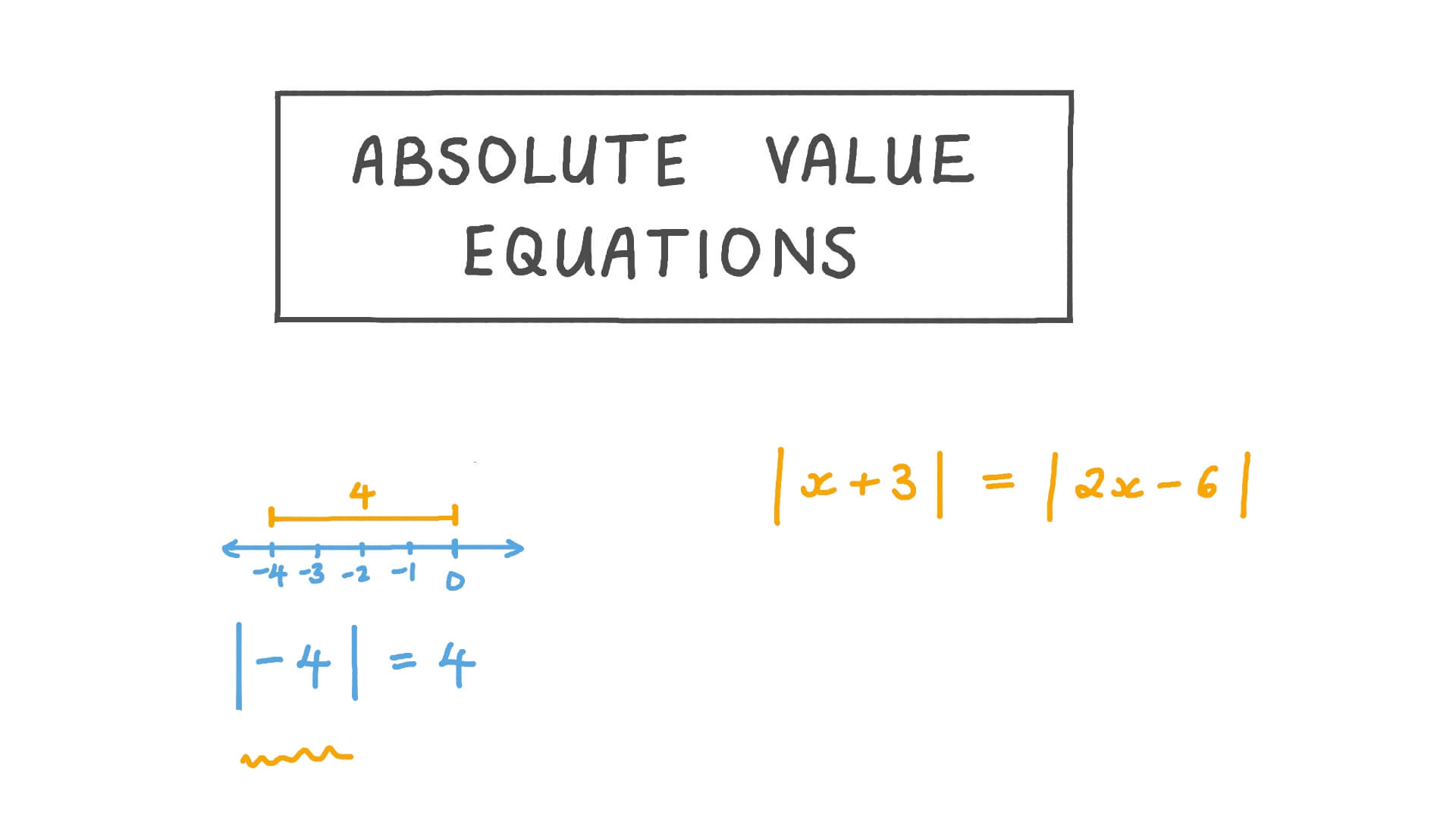
+
No, the absolute value of any number is always non-negative because it measures the distance, which is inherently positive or zero.
How can I solve an equation with absolute values?

+
When solving equations with absolute values, consider both the positive and negative cases of the expression inside the absolute value. For example, solve |x| = 2 by solving x = 2 and x = -2.