9 Essential Multiplication Facts for Quick Learning

Mastering multiplication facts is an important skill that provides the groundwork for various mathematical concepts, including division, algebra, and even understanding more complex financial mathematics. Whether you're helping a young learner or brushing up on your arithmetic skills, understanding and quickly recalling essential multiplication facts can significantly enhance calculation speed and boost confidence in math. Here are 9 key multiplication facts that can accelerate the learning curve for students.
1. The Commutative Property of Multiplication

The first essential fact is the commutative property of multiplication, which states that the order of factors does not affect the product:
- Example: 3 × 4 = 4 × 3
This property reduces the number of facts to learn by half, as you only need to know one combination of each pair of numbers.
2. Multiplying by Zero

Any number multiplied by zero equals zero. This fundamental rule should be one of the first to commit to memory:
- Example: 7 × 0 = 0
This principle can be particularly useful when simplifying expressions or solving equations.
3. Multiplying by One

Multiplying any number by one gives the number itself:
- Example: 5 × 1 = 5
While this fact seems trivial, it's vital for understanding concepts like identity elements in algebra.
4. The Multiplication Table of 2

The table of 2 is typically one of the easiest to remember because doubling numbers is a straightforward operation:
| 2 × 1 | 2 |
|---|---|
| 2 × 2 | 4 |
| 2 × 3 | 6 |
| 2 × 4 | 8 |
| 2 × 5 | 10 |

The pattern continues, with even results every time.
5. Multiplying by Five

The multiplication facts of 5 can often be derived from the multiplication table of 2. If you double the table of 2 and then halve it, you get the table of 5:
- Example: 2 × 2 = 4, then 4 × 2 = 8, and finally 8 ÷ 2 = 4, so 5 × 2 = 10
This method can be particularly handy for quick mental calculations.
6. Multiplying by Ten
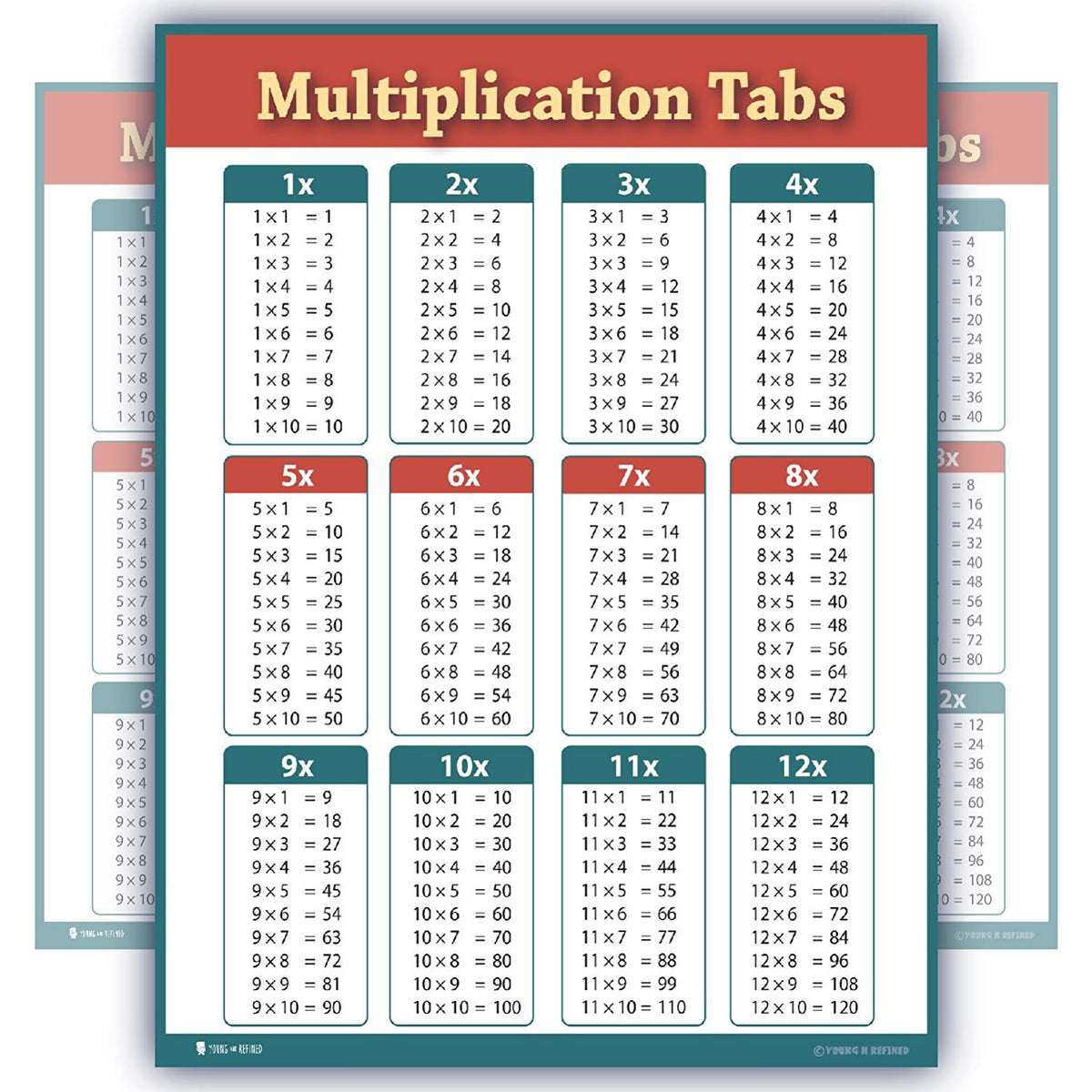
Multiplying any number by ten simply involves adding a zero to the number:
- Example: 3 × 10 = 30
This rule is intuitive and fundamental for understanding place value.
7. Understanding Squares

The multiplication facts involving squares (i.e., a number multiplied by itself) are crucial because:
- Example: 3 × 3 = 9
These squares form the basis for understanding the geometry of squares and cuboids, as well as algebra and calculus.
8. Factoring and the Distributive Property

Understanding how to use the distributive property can simplify multiplication:
- Example: 4 × (6 + 2) = (4 × 6) + (4 × 2) = 24 + 8 = 32
This property allows you to break down complex multiplication problems into smaller, more manageable parts.
9. The Doubling Strategy

Doubling a number is a strategy often used for quick mental multiplication:
- Example: 2 × 6 = 12, 4 × 6 = 2 × (2 × 6) = 2 × 12 = 24
By learning to double numbers, you can quickly solve many multiplication facts.
Incorporating these multiplication facts into learning routines will enhance computational fluency and lay a robust foundation for more advanced mathematical operations. Practice with flashcards, worksheets, or simple daily problems can reinforce these facts, making them second nature. However, it's important not just to memorize but to understand why these rules work, which fosters deeper mathematical understanding.
👉 Note: Encourage learners to use visual aids like number lines or arrays to see the multiplication process visually, which can aid in comprehension and retention.
To wrap up, these multiplication facts serve as crucial stepping stones for mastering arithmetic, which in turn forms the basis for all future mathematical learning. By focusing on these fundamentals, students can build confidence and a solid mathematical foundation that will serve them well beyond the classroom.
Why is it important to memorize multiplication facts?

+
Memorizing multiplication facts allows for quick mental calculation, reduces cognitive load when solving more complex problems, and provides a solid foundation for understanding algebra, fractions, and higher math.
What techniques can help in memorizing multiplication facts?

+
Techniques include using flashcards, engaging in repetitive practice, teaching the facts to others, playing math games, and using visual or physical models like multiplication arrays or Cuisenaire rods.
Can calculators replace the need to know multiplication facts?

+
While calculators can perform calculations, understanding basic arithmetic is still essential for building number sense, problem-solving skills, and for performing quick mental math which is often needed in everyday life.



