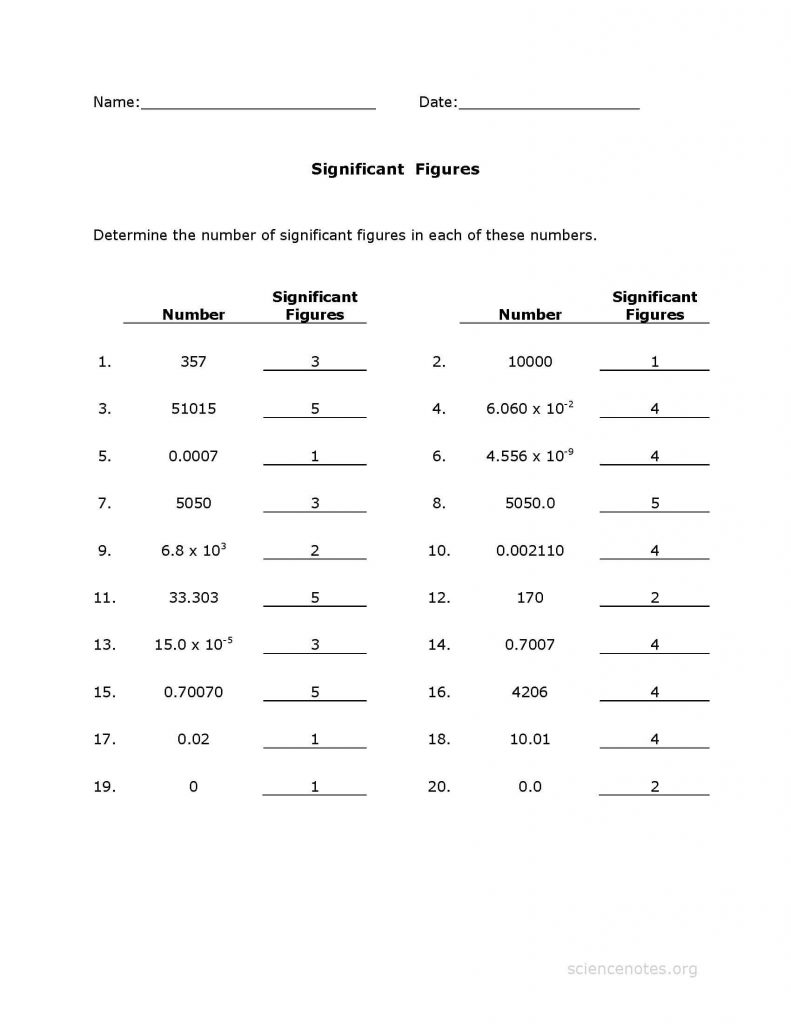
8th Grade Math Slope Worksheets: Master the Basics!

Mastering the concept of slope is a fundamental step in your 8th-grade math journey. Slope represents how steep a line is, and understanding this idea can unlock many doors in algebra and beyond. Whether you're preparing for an exam or just looking to reinforce your math skills, our carefully curated slope worksheets are designed to help you grasp this concept effectively.
Understanding Slope: The Basics

Before diving into the worksheets, let's solidify your understanding of slope:
- Definition: Slope is the measure of the steepness of a line, usually denoted by the letter m.
- Formula: The slope between two points (x_1, y_1) and (x_2, y_2) is given by: \[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
- Types of Slopes:
- Positive Slope: Line slopes upward from left to right.
- Negative Slope: Line slopes downward from left to right.
- Zero Slope: The line is horizontal with no rise over run.
- Undefined Slope: The line is vertical with run equaling zero.
- Graphical Interpretation: A line with a slope of 2/3 means for every 3 units you move to the right, you move up by 2 units.
🔍 Note: The slope gives us an instant snapshot of how a line behaves, making it a key concept in understanding linear equations.
Practicing with Slope Worksheets

Here are some types of slope worksheets you might encounter, along with their benefits:
1. Basic Slope Worksheets


- Find the slope using two given points.
- Determine if the slope is positive, negative, or zero.
- Identify whether the slope is undefined.
2. Graph-Based Slope Worksheets


- Plot points and calculate the slope from the graph.
- Identify slopes from different lines on a coordinate plane.
- Determine if lines are parallel (same slope), perpendicular (negative reciprocal slopes), or neither.
3. Real-World Slope Applications

- Calculate slope from real-life scenarios like ramp gradients or hiker’s trails.
- Apply slope in physics or engineering problems.
4. Mixed Practice Worksheets

- Find slopes with different types of coordinates.
- Match slopes to lines on a graph.
- Convert between slope-intercept form (y = mx + b) and standard form of linear equations.
⚙️ Note: Practice with a variety of problem types will enhance your adaptability and understanding of slope in different contexts.
Steps to Master Slope
To truly master the concept of slope, follow these steps:
- Understand the Formula: Memorize and understand the slope formula to quickly calculate slopes.
- Practice with Points: Regularly solve problems using pairs of points.
- Work on Visualizing Slopes: Sketch lines to visualize what different slopes look like on a graph.
- Relate to Real Life: Look for slope in everyday situations to reinforce the concept.
- Use Worksheets for Practice: Consistent practice with different types of worksheets will strengthen your skills.
📚 Note: Regularly revisiting worksheets and real-life problems will help in solidifying the concept of slope.
To truly master slope, follow these steps:
In our journey to understand slope, we’ve explored its definition, the different types, and how to practice with dedicated worksheets. Slope, while a basic concept, has far-reaching implications in algebra, geometry, and real-world applications. By mastering it, you set a strong foundation for more complex mathematical concepts. Keep practicing with a variety of problems, visualize the slopes, and relate them to real-life scenarios to solidify your understanding.
Why is slope important in mathematics?

+
Slope is crucial as it helps us understand the rate of change, the steepness of lines, and the relationship between two sets of data. It’s a fundamental concept in algebra, geometry, and calculus.
How can I remember the slope formula?

+
Think of it as “rise over run.” Use mnemonic devices like “rice” (rise) and “rice cooker” (run). Alternatively, you can use “up over right” to remember the fraction.
What’s the difference between positive and negative slopes?

+
A positive slope means the line ascends from left to right, indicating an increase. A negative slope means the line descends from left to right, indicating a decrease.
Can a line have a slope of zero?

+
Yes, a line with a slope of zero is a horizontal line. It has no vertical change, hence no “rise.”
What does an undefined slope mean?

+
An undefined slope means the line is vertical, and you cannot calculate the slope because there’s no horizontal change, or “run,” involved.