5 Quick Synthetic Division Techniques for Worksheets

In the vast world of mathematics, division has always held a special place due to its ubiquitous applications. However, when it comes to higher-level algebra, specifically polynomials, traditional division methods can quickly become cumbersome. This is where synthetic division emerges as a streamlined and efficient technique. In this blog post, we delve deep into five synthetic division techniques that can revolutionize how students and educators approach division worksheets. Whether you're a student struggling with polynomial division or an educator looking to enhance your teaching techniques, these methods will provide clarity and efficiency.
The Basics of Synthetic Division

Before diving into specific techniques, let’s understand what synthetic division is:
- Definition: Synthetic division is a shorthand method of dividing a polynomial by a linear factor of the form (x - c).
- Process: It involves writing down coefficients, performing series of multiplications, and additions rather than the traditional long division method.

Technique #1: Basic Synthetic Division Setup

To set up for synthetic division:
- Write the divisor in the form of (x - c).
- List the coefficients of the polynomial.
- Set up a table where the divisor is placed outside, and coefficients go inside.
📝 Note: This technique is fundamental for understanding more complex applications of synthetic division.
Technique #2: Coefficients Only Technique
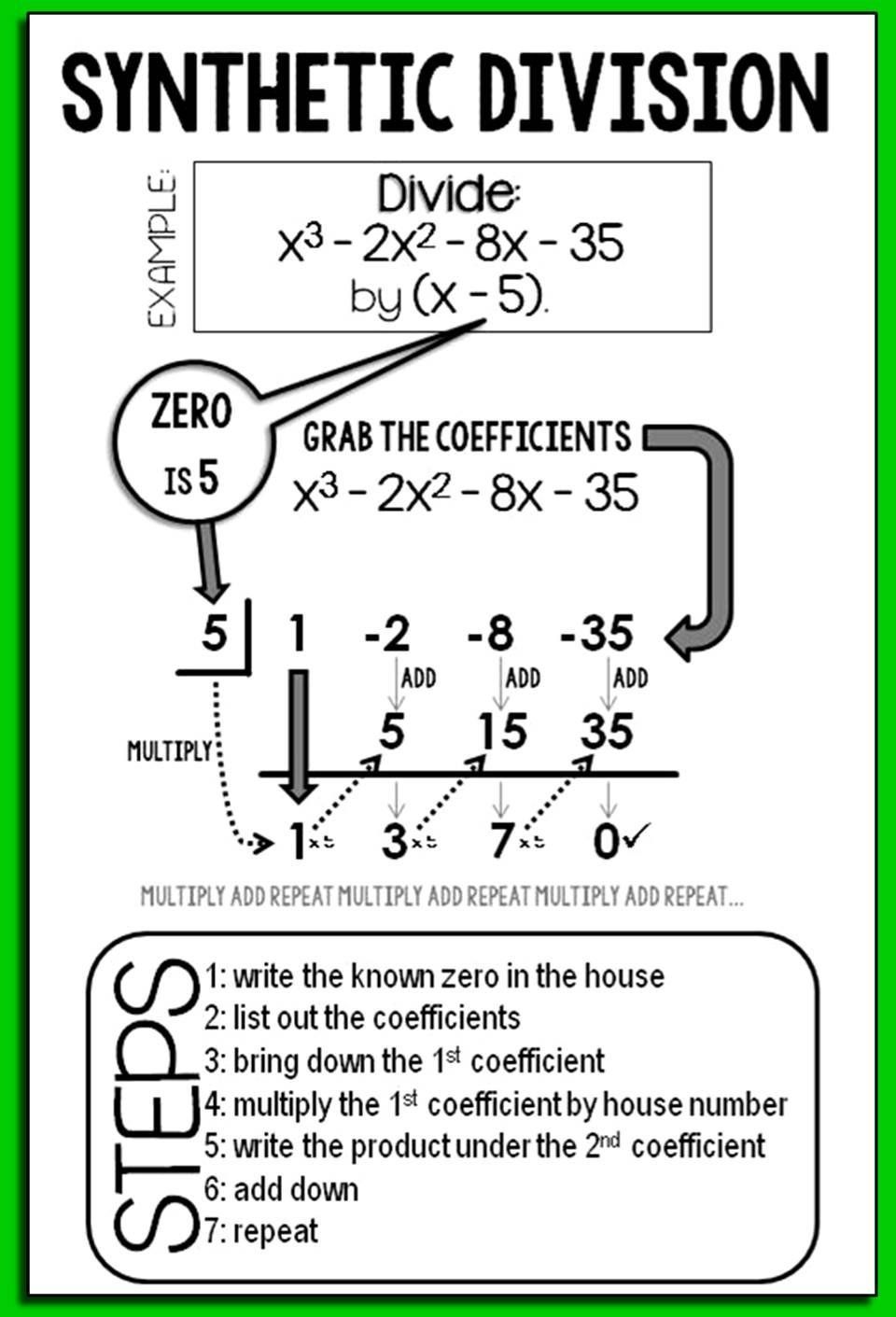
This method further simplifies synthetic division by focusing solely on the coefficients:
- Ignore the variables and their powers; work with the coefficients only.
- Align the coefficients under the division line, then proceed with the synthetic division steps.
Technique #3: Use of Zero Coefficients

When a polynomial has missing terms:
- Fill the gaps with zero coefficients to complete the degree of the polynomial.
- This ensures the integrity of the division process.
Technique #4: The Remainder Theorem Connection

Integrating synthetic division with the Remainder Theorem:
- The last value in synthetic division gives the remainder when the polynomial is divided by (x - c).
- This can be used to quickly determine if a given linear factor is actually a factor.
Technique #5: Backwards Synthetic Division

A less common but useful approach:
- Instead of dividing, multiply to reconstruct the polynomial.
- It’s particularly useful for verifying solutions or creating practice problems.
Mastering synthetic division through these techniques can significantly reduce the time spent on polynomial division, enhance conceptual understanding, and make solving complex algebraic problems more manageable. Here are some final thoughts on applying these techniques:
Each of these methods offers a unique angle on synthetic division, not just in terms of efficiency but also in deepening mathematical understanding:
- Conceptual Clarity: By working with only coefficients or zero coefficients, students can see the polynomial's behavior and structure more clearly.
- Efficiency: These techniques cut down on computational time, making division worksheets less daunting and more accessible.
- Verification and Learning: Using backwards synthetic division provides an excellent tool for self-assessment and for educators to craft insightful learning experiences.
As we conclude, remember that synthetic division is not just a calculation tool but a gateway to understanding polynomial behavior, factorability, and the relationship between the coefficients of polynomials and their roots. Practice these techniques, explore their applications, and watch as algebraic division transforms from a complex task to an elegant part of your mathematical toolkit.
What is synthetic division?

+
Synthetic division is a shorthand method to divide a polynomial by a linear binomial, specifically in the form of (x - c), where ‘c’ is a constant. It uses only the coefficients of the polynomial, making the process simpler and less time-consuming compared to long division.
Why use synthetic division instead of long division?

+
Synthetic division is much quicker for dividing polynomials by linear factors because it eliminates the need for writing variables and their exponents, reducing errors and calculation time.
Can synthetic division be used for all polynomial divisions?

+
No, synthetic division is most effective when dividing by linear polynomials of the form (x - c). For division by polynomials with higher degrees, traditional polynomial long division is typically required.