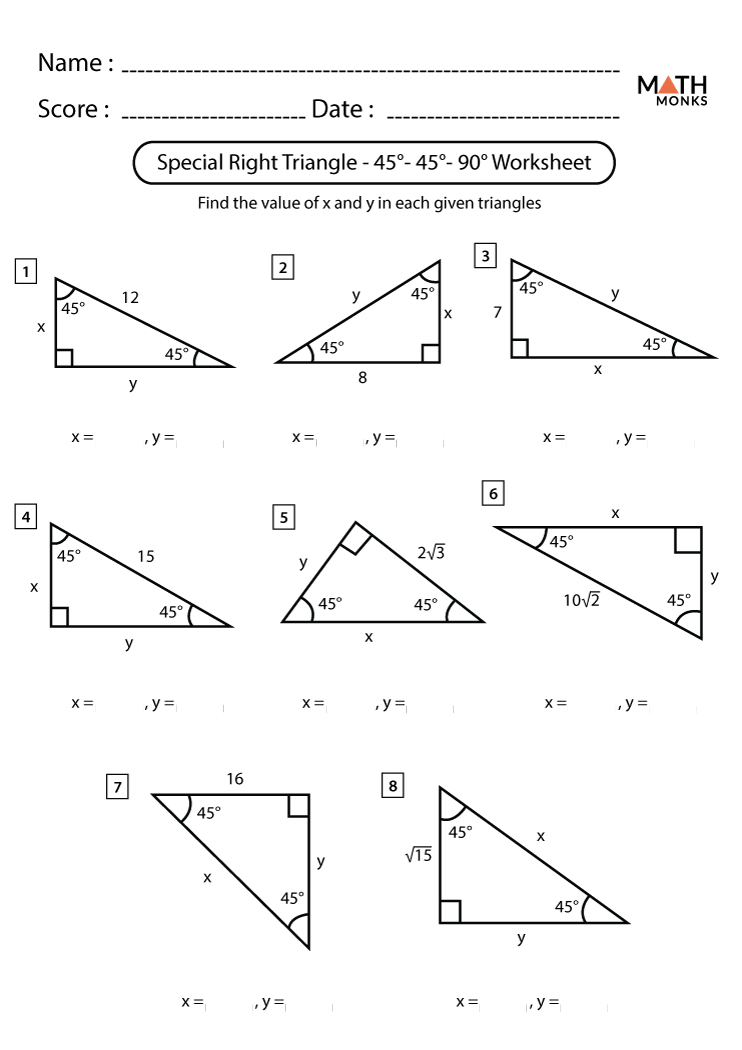
5 Key Tips for Solving Special Right Triangles

When dealing with mathematics and particularly geometry, special right triangles stand out due to their unique properties that simplify many complex problems. Whether you're preparing for an exam, helping a student, or merely looking to brush up on your geometry skills, understanding these triangles can significantly enhance your problem-solving toolkit. Here are five key tips to master the art of solving special right triangles:
1. Recognize the Types

Not all triangles are created equal, especially when it comes to special right triangles. The three most common types you should be familiar with are:
- 45-45-90 Triangle: Both legs are equal, and the hypotenuse is √2 times the length of each leg.
- 30-60-90 Triangle: One angle is 30°, another is 60°, and the sides are related with the ratio 1:√3:2, where the hypotenuse is twice the shortest leg.
- Isosceles Right Triangle: This is essentially the same as a 45-45-90 triangle, where all sides follow the same ratio.
Identifying which type of triangle you’re dealing with is the first step in solving the problem effectively.

2. Use the Pythagorean Theorem

The Pythagorean theorem, (a^2 + b^2 = c^2), is your best friend when dealing with right triangles. While special right triangles have their own sets of ratios, for verification or solving less conventional problems, this theorem is always applicable:
- For a 45-45-90 triangle, if the legs are (a), then the hypotenuse is (a√2).
- For a 30-60-90 triangle, if the shortest side is (a), then the hypotenuse is (2a), and the other leg is (a√3).
Knowing these relationships by heart will streamline your calculations.
3. Practice with Ratios

Memorize the side ratios for special right triangles to solve problems quickly:
| Triangle Type | Side Lengths |
|---|---|
| 45-45-90 | 1 : 1 : √2 |
| 30-60-90 | 1 : √3 : 2 |
| Isosceles Right | 1 : 1 : √2 |

📐 Note: These ratios are always true regardless of the size of the triangle.
4. Apply Trigonometric Functions
While ratios help in straightforward problems, trigonometric functions can be crucial for more complex scenarios involving angles other than the standard ones in special right triangles:
- Sine (sin) - Opposite/Hypotenuse
- Cosine (cos) - Adjacent/Hypotenuse
- Tangent (tan) - Opposite/Adjacent
For special triangles, these values can often be derived from the given ratios. For example, in a 30-60-90 triangle, sin(30°) = 0.5, cos(60°) = 0.5, and tan(30°) = 1/√3.
5. Simplify Complex Problems with Geometry

Not all problems will fit neatly into the known ratios of special right triangles. However, by using the principles of these triangles, you can break down complex geometric shapes into simpler forms:
- Break down a larger triangle into multiple right triangles.
- Identify patterns or symmetries that can be used to solve problems more efficiently.
By recognizing the parts that make up the whole, you can apply special triangle rules to solve intricate problems more straightforwardly.
Mastering these five tips for solving special right triangles can transform how you approach geometry problems. Whether you're solving for side lengths, angles, or verifying identities, these strategies provide a structured way to tackle various mathematical challenges. Understanding the types, using the Pythagorean theorem, knowing the ratios, applying trigonometry, and leveraging geometry will equip you with a robust toolkit for any geometry problem involving right triangles.
What if I encounter an angle not present in standard special right triangles?

+
You can use trigonometric functions or the principles of similar triangles to find side lengths or angles that aren’t standard in special right triangles.
Can I use these tips for non-right triangles?

+
These tips are specifically designed for right triangles, but understanding special right triangles can aid in solving other types through geometry or trigonometry.
How do I memorize the ratios effectively?

+
Practice is key. Flashcards, repetitive drills, and visual aids like triangle models can help. Also, understanding the derivation of these ratios might help in memorization.
Why are special right triangles important in math?

+
They simplify the solving of many geometry and trigonometry problems, making them foundational for understanding more complex mathematical concepts.
Do these rules apply to all right triangles?
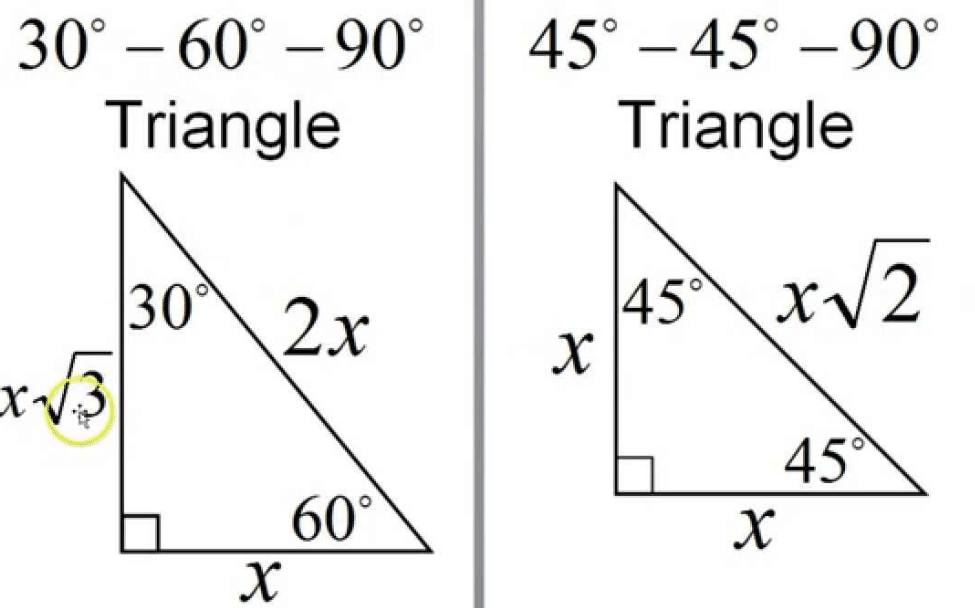
+
Special right triangles follow specific ratios due to their angles. Other right triangles can be analyzed with general trigonometry and the Pythagorean theorem.



