5 Essential Tips for Mastering 45-45-90 Triangles

In the study of geometry, mastering triangles is crucial, particularly for standardized tests like the SAT and ACT where understanding the properties of specific triangles can save time and increase accuracy. One such essential triangle is the 45-45-90 triangle, also known as an isosceles right triangle. Here, we will dive into the essentials of this triangle, providing you with five fundamental tips to grasp its geometry effectively.
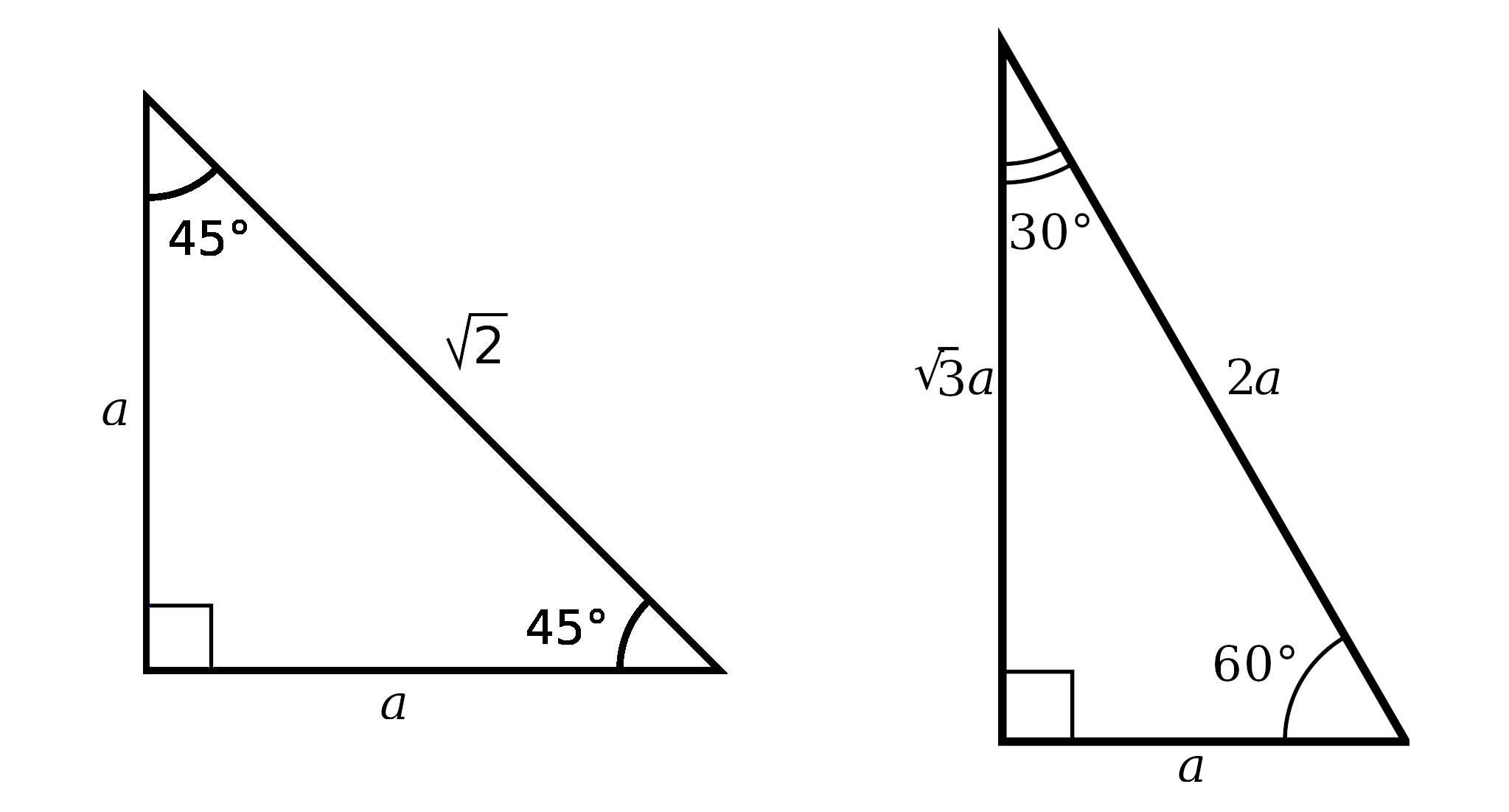
Understanding the Basics

Before delving into specific strategies, understanding the core characteristics of a 45-45-90 triangle is essential:
- Angles: It has one right angle (90°) and two angles of 45° each.
- Sides: The sides opposite the 45° angles are equal, and the hypotenuse, which is opposite the right angle, has a unique relationship to these legs.
- Relationship: The hypotenuse is √2 times the length of each leg.
Tip 1: Use the 45-45-90 Triangle Theorem

The theorem for a 45-45-90 triangle states:
- If the legs are equal in length, then the hypotenuse is leg * √2.
Here’s how you can utilize this:
- Suppose one leg is given as x. The other leg will also be x, and the hypotenuse will be x√2. This ratio simplifies calculations in various geometric problems.
- Example: If a leg of the triangle is 5 units, the hypotenuse will be 5√2 units.
Tip 2: Memorize Common Values

Memorizing the side lengths for common values simplifies mental calculations:
| Legs | Hypotenuse |
|---|---|
| 1 | √2 |
| √2 | 2 |
| 2 | 2√2 |
| 5 | 5√2 |
By memorizing these, you’ll save time during exams or quick mental calculations.
Tip 3: Trigonometric Ratios Made Easy

Given that the angles in a 45-45-90 triangle are so specific, trigonometric functions have a simplified form:
- Sine and Cosine: For either 45° angle, sin(45°) = cos(45°) = √2/2.
- Tangent: tan(45°) = 1.
This simplifies problems involving trigonometry significantly:
- Example: If you need to find the sine or cosine of either 45° angle, you just use √2/2, which can simplify trigonometric calculations in physics or engineering problems.
Tip 4: Visualize the Triangles

Visualizing 45-45-90 triangles helps in understanding their properties:
- Draw a square, then draw its diagonal. Each half of the square forms two right triangles, which are identical 45-45-90 triangles. This visual representation helps in grasping the side relationships.
- Imagine rotating one of these triangles so that the hypotenuse becomes the base of a new right triangle, again reinforcing the symmetry and equality of the sides opposite the 45° angles.
📝 Note: Drawing and visualizing triangles can greatly enhance your spatial reasoning, which is crucial for geometry problems.
Tip 5: Practice with Real-World Applications

Applying 45-45-90 triangles to real-life scenarios can make their study more engaging:
- Architecture: In designing structures with diagonal bracing.
- Landscaping: When creating symmetrical features like a patio or pool area where the dimensions need to be precise.
- Navigation: Pilots and sailors often use these triangles for bearings and distances when making a 45-degree turn.
By linking these triangles to real-world scenarios, you’ll find memorizing and understanding their properties more enjoyable and relatable.
To summarize, mastering the 45-45-90 triangle involves understanding its basic properties, utilizing its theorem, memorizing key values, simplifying trigonometric calculations, visualizing its form, and applying it to real-life situations. These steps not only equip you with the knowledge to excel in geometry but also provide a practical understanding that can be used in various fields. The beauty of this triangle lies in its symmetry and the simplicity of its mathematics, making it an excellent starting point for anyone diving into the geometric world.
Why are 45-45-90 triangles important?

+
These triangles are fundamental in various mathematical and real-world applications due to their symmetry and the ease with which their properties can be understood and applied.
How can I quickly recognize a 45-45-90 triangle?

+
Look for two equal sides or two angles of 45 degrees each. If any of these conditions are met, you’re looking at a 45-45-90 triangle.
Can the hypotenuse ever be shorter than the legs?
+
No, in a 45-45-90 triangle, the hypotenuse is always the longest side due to the Pythagorean theorem and the special ratio involved.