45-45-90 Triangle Day 1: Easy Worksheet Answers

The concept of the 45-45-90 triangle is fundamental in geometry and plays a critical role in trigonometry, architecture, and engineering. These triangles are known for their special properties, which make calculations simpler when compared to other triangles. In this post, we'll delve into an easy worksheet focusing on these triangles, providing detailed answers and explanations to solidify your understanding.
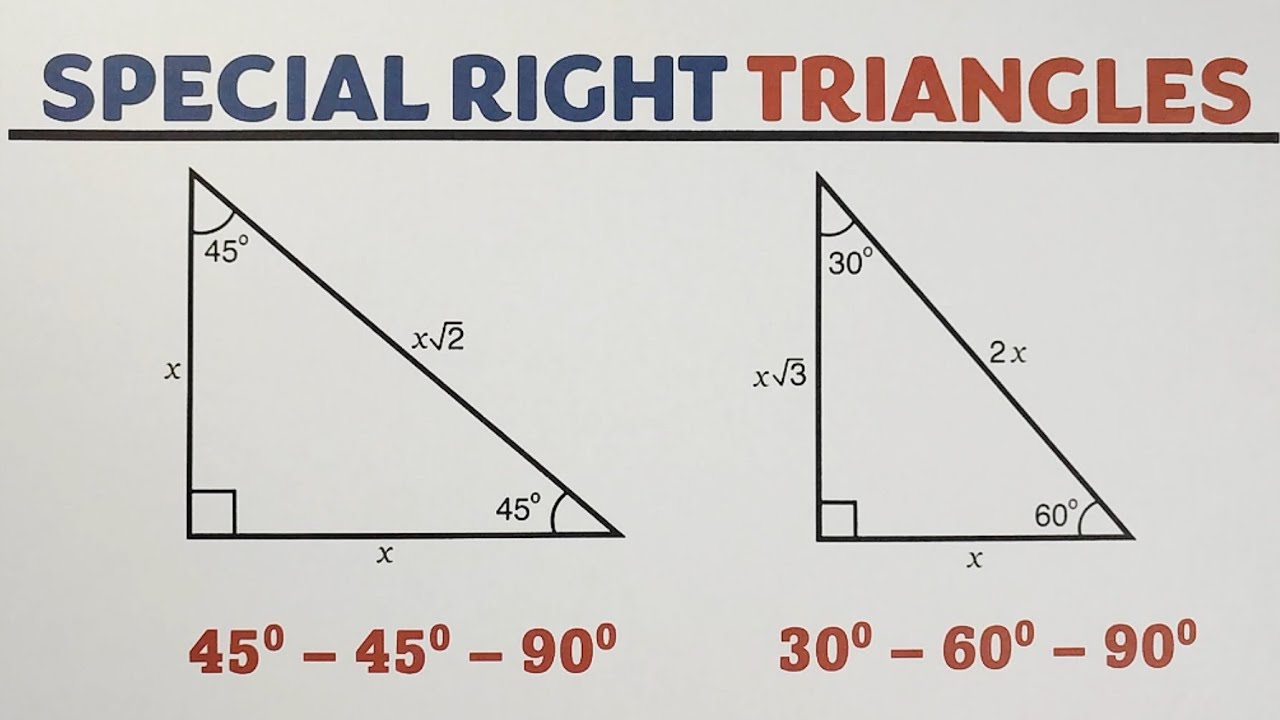
Understanding the 45-45-90 Triangle

Before diving into the worksheet, let's review what makes a 45-45-90 triangle unique:
- The triangle's angles are 45 degrees, 45 degrees, and 90 degrees.
- The legs are of equal length.
- The hypotenuse is always √2 times the length of each leg.

Worksheet Overview

Here's an example worksheet that we will explore:
| Problem | Answer | Explanation |
|---|---|---|
| 1. If a leg of a 45-45-90 triangle is 5 units, what is the hypotenuse? | 5√2 units | In a 45-45-90 triangle, the hypotenuse (H) is always √2 times the length of a leg (L): H = L * √2 = 5 * √2. |
| 2. Find the length of one leg if the hypotenuse is 10 units. | 5√2/2 units | Given H = L√2, solve for L: L = H/√2 = 10/√2 = 5√2/2. |

Problem Solving
Let's go through the worksheet problems step-by-step:
- Problem 1: Given one leg is 5 units, the hypotenuse is calculated as 5 * √2.
- Problem 2: When the hypotenuse is 10 units, divide by √2 to find the length of one leg.
📝 Note: Always simplify your answers when possible to enhance understanding and avoid errors in calculation.
Further Applications

Understanding the properties of 45-45-90 triangles can benefit you in various fields:
- Architecture: For designing symmetrical structures and stairs.
- Engineering: In creating precise measurements for machinery and buildings.
- Mathematics: Simplifying calculations in trigonometry.
Incorporating the principles of the 45-45-90 triangle into your design and calculation processes can lead to more efficient and accurate results. Remember, these triangles can be scaled up or down, maintaining their properties, making them versatile in practical applications.
In our exploration of 45-45-90 triangles, we've covered foundational aspects that are crucial not only for solving basic geometry problems but also for applying in real-world scenarios. By understanding how to calculate the sides of these triangles, you've equipped yourself with tools that can be used in various fields. From architecture to engineering, the simplicity and regularity of these triangles make them an indispensable part of design and problem-solving. Remember to simplify your calculations and keep an eye out for opportunities where the 45-45-90 triangle properties can simplify complex problems.
What is the significance of the 45-45-90 triangle?

+
These triangles are significant because their angles and sides have predictable relationships, making calculations easier in geometry and trigonometry.
Can 45-45-90 triangles be isosceles?

+
Yes, 45-45-90 triangles are always isosceles because the two legs are always of equal length.
How can knowing the properties of 45-45-90 triangles help in everyday life?

+
From designing symmetrical structures to calculating the height of a staircase, these triangles are practical tools in daily problem-solving.