3D Pythagorean Theorem Worksheet for All Skill Levels

If you find any errors or things that need clarification, please leave a comment below.
Understanding the Pythagorean Theorem in Three Dimensions

The Pythagorean Theorem, often referred to as the "cornerstone" of geometry, is an age-old principle that holds for any right triangle. Its basic form states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides:
\[ c^2 = a^2 + b^2 \]
However, when we delve into three dimensions, this theorem takes on a slightly different form, expanding our geometric toolkit and allowing for the solving of spatial problems. Let's explore how the Pythagorean Theorem is applied to 3D structures, providing insights for students from beginners to advanced learners.
Basic Principles of the 3D Pythagorean Theorem

In three-dimensional space, we often deal with rectangular prisms, triangular prisms, pyramids, and other polyhedrons. Here's how the Pythagorean Theorem is applied:
- Rectangular Prism: Consider a rectangular prism with side lengths a, b, and c. The longest diagonal across the prism, which spans from one corner to the opposite corner, can be found using the 3D extension of the theorem:
\[ d = \sqrt{a^2 + b^2 + c^2} \]
- Other Solids: For triangular prisms or pyramids, we can extend this principle by considering the diagonal of a face as one side of a right triangle whose legs are the edges of the base. The other leg would be the height of the prism or the altitude from the apex to the base.
3D Pythagorean Theorem Worksheet for Beginners
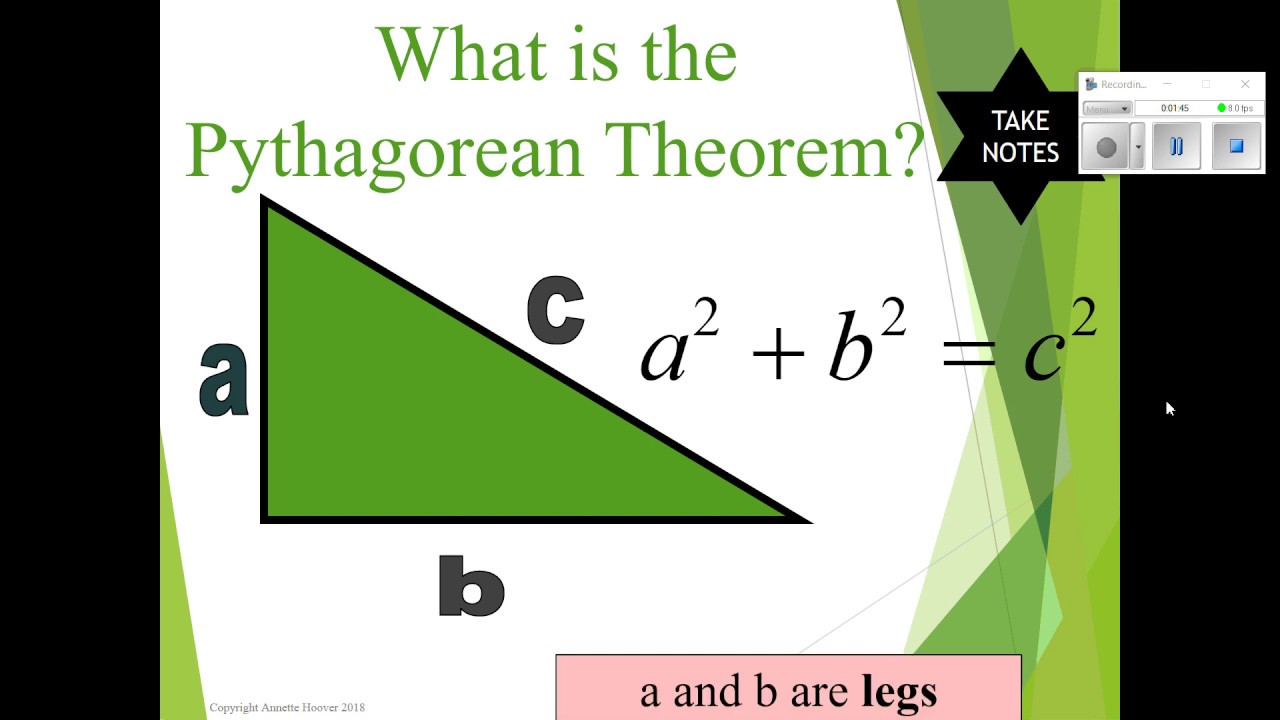
For beginners, understanding the basic applications of the 3D Pythagorean Theorem is crucial. Here's a simple worksheet to help:
- Calculate the diagonal of a cube with side length 5 units.
- Find the diagonal of a rectangular prism where the sides are 4, 5, and 6 units.
- A triangular prism has a base with sides of 3 and 4 units, and a height of 12 units. Find the diagonal from one base corner to the opposite base corner.
Intermediate Skill Level

At an intermediate level, students should understand how to manipulate the theorem:
- Given two diagonals in the plane of one face of a rectangular prism, calculate the length of the third diagonal through the volume.
- Determine the height of a pyramid if the base is a square with a side length of 10 units, and the slant height from the apex to the midpoint of one side of the base is 12 units.
- If the volume of a pyramid is 120 cubic units and the base area is 36 square units, find the slant height.
Advanced Applications

Advanced problems incorporate not only the Pythagorean Theorem but also other geometric principles:
- Problem 1: A rectangular prism has face diagonals of 7 units, 8 units, and 9 units. Calculate its volume.
- Problem 2: If the space diagonal of a cube is 10 units, what is the edge length of the cube?
- Problem 3: Prove that the diagonals of a regular hexahedron (cube) are equal to each other.
Using the 3D Pythagorean Theorem in Real-Life Scenarios

Here are some practical applications:
- Architecture: To calculate the roof pitch or the diagonal support beams needed in a building.
- Carpentry: For precise cutting and fitting of wood for structures like staircases or furniture.
- Surveying: To find the shortest distance between two points when direct measurement is not possible.
- Engineering: To design 3D structures, like pipelines or machines, where precise calculations are essential for efficiency and safety.
Here's a table summarizing typical real-life applications of the 3D Pythagorean Theorem:
| Industry | Application |
|---|---|
| Construction | Measuring heights of structures or distances within a building |
| Video Games | Creating realistic environments and calculating distances for game physics |
| Aerospace | Finding distances for satellite trajectories and positioning |
| Navigation | Calculating the shortest flight paths or travel routes |

📚 Note: The 3D Pythagorean Theorem provides a fundamental tool for understanding distances in three-dimensional space, but always consider the context of the problem to ensure your calculation matches the real-world scenario.
As we've delved into the intricacies of the 3D Pythagorean Theorem, it's clear that this mathematical principle extends far beyond simple 2D shapes. From construction to virtual reality, from engineering design to artistic visualization, understanding the Pythagorean Theorem in three dimensions not only equips you with a valuable mathematical tool but also opens up a world of problem-solving possibilities. Whether you're calculating diagonal support beams for a skyscraper or navigating a complex virtual environment, this theorem is fundamental to your analytical toolkit.
Can the 3D Pythagorean Theorem be used for any shape?

+
The theorem can be applied to polyhedrons with right angles, or it can be used to calculate distances between points in space, not just within regular geometric shapes.
How does the 3D Pythagorean Theorem relate to vectors?

+
The theorem is essentially the magnitude of the vector sum of the side lengths in three-dimensional space. It’s the basis for calculating vector lengths and distances between points in 3D.
What are common mistakes when using the 3D Pythagorean Theorem?

+
Errors often arise when dimensions are mixed up, calculations are not checked for consistency, or when the shape’s context is ignored leading to incorrect applications.
Why is it important to learn the 3D Pythagorean Theorem?

+
It’s not just about solving mathematical problems; it’s crucial for understanding spatial relationships, designing efficient structures, and navigating in virtual or physical 3D environments.