5 Steps to Solve 30 60 90 Triangles Worksheet Answers

Geometry often presents students with various challenges, one of which is understanding and solving problems related to specific types of triangles. Among these, the 30-60-90 triangle stands out due to its unique properties. This triangle, also known as a special right triangle, has angles that are precisely 30 degrees, 60 degrees, and 90 degrees. Today, we'll delve into five practical steps to work through the "30-60-90 triangles worksheet answers" effectively, ensuring that students can grasp this concept with ease.
Step 1: Understanding the 30-60-90 Triangle


Before diving into solving problems, it’s crucial to understand the characteristics of the 30-60-90 triangle:
- The shortest side is always opposite the 30-degree angle.
- The longest side, or hypotenuse, is opposite the 90-degree angle and is twice the length of the shortest side.
- The side opposite the 60-degree angle is equal to the hypotenuse multiplied by the square root of 3 divided by 2.
This foundational knowledge is essential for accurately solving the worksheet.
Step 2: Identify the Knowns and Unknowns
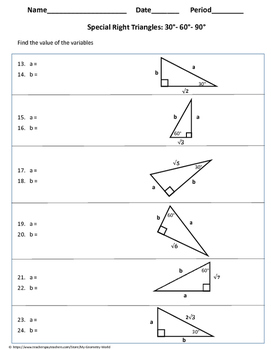
When approaching problems in your 30-60-90 triangle worksheet, start by:
- Noting which sides of the triangle are given.
- Identifying which side(s) you need to find.
- Marking the known values on your diagram.
Here’s an example:
| Side | Value |
|---|---|
| Shortest side (opposite 30°) | Given |
| Hypotenuse | Unknown |
| Side opposite 60° | Unknown |

💡 Note: Always ensure you have at least one side length to proceed with your calculations.
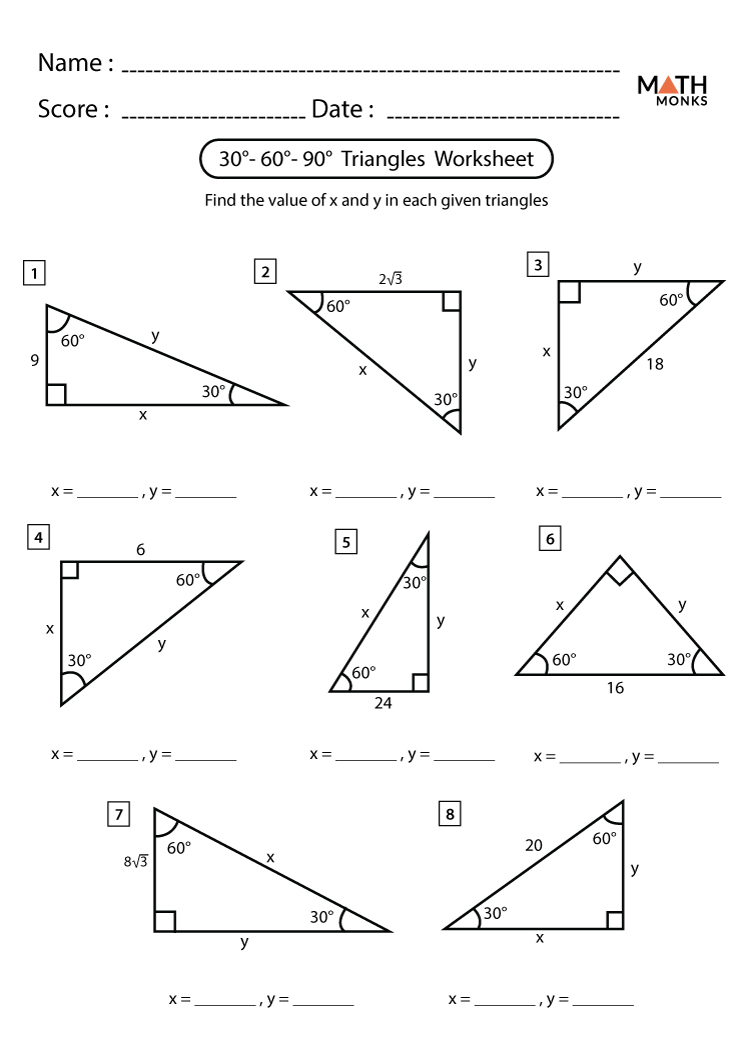
Step 3: Use Ratios to Find Missing Sides

The ratios in a 30-60-90 triangle are crucial:
- Shortest side (x): If given, this side helps you find other sides.
- Hypotenuse: Twice the shortest side.
- Side opposite 60°: Hypotenuse multiplied by √3/2.
For instance, if the shortest side is 4 units:
- Hypotenuse = 4 * 2 = 8 units
- Side opposite 60° = 4 * √3
This step allows you to fill in any missing side lengths efficiently.
Step 4: Apply the Pythagorean Theorem

In instances where only two sides are known, or you need to confirm your calculations:
- Use the Pythagorean Theorem (a² + b² = c²), where:
- ‘a’ and ‘b’ are the lengths of the legs of the triangle, and
- ‘c’ is the hypotenuse.
This can act as a double-check or help when the ratios are not straightforward.
Step 5: Review and Cross-check

Finally, ensure your calculations are correct by:
- Rechecking your steps and ratios.
- Using the Pythagorean Theorem to verify the triangle’s integrity.
- Comparing your answers with the provided answer key if available.
This step is vital for ensuring accuracy and understanding where you might have gone wrong if there are discrepancies.
By following these five steps, you'll find yourself confidently navigating through any 30-60-90 triangle problems. Remember, the key lies in understanding the triangle's properties, applying the right mathematical principles, and reviewing your work carefully. Mastering these triangles not only helps with geometry but also enhances your overall mathematical ability, as these triangles are often used as building blocks for more complex problems.
What if I’m given only the hypotenuse in a 30-60-90 triangle?
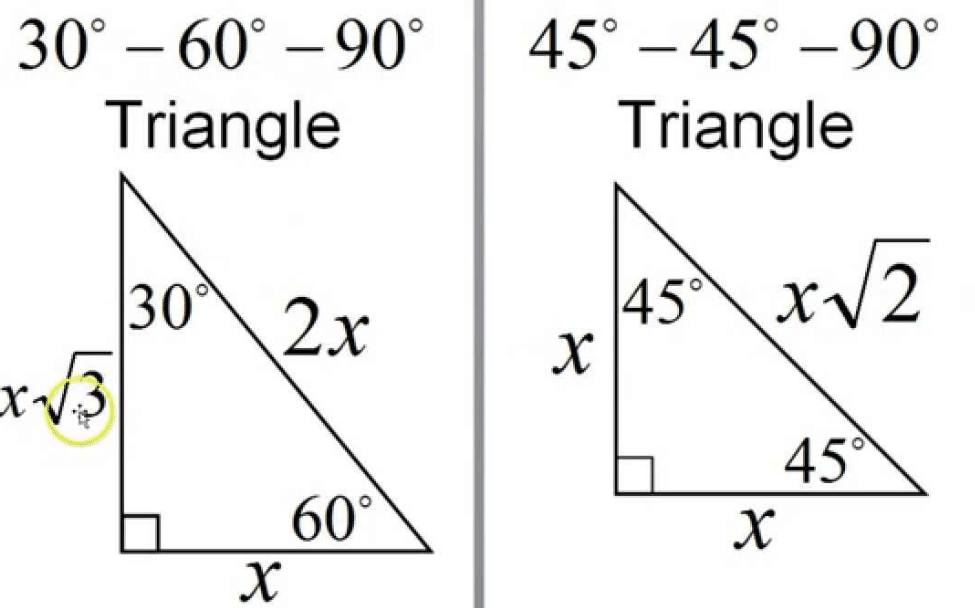
+
If you’re given the hypotenuse, divide it by 2 to find the shortest side (opposite 30°). Then, the side opposite the 60° angle would be the shortest side multiplied by √3.
How do I know if my calculations are correct?

+
You can verify your calculations by using the Pythagorean Theorem or by comparing your answers to an answer key if available. Additionally, check if the ratios are consistent with those of a 30-60-90 triangle.
Can the 30-60-90 triangle rule be applied to all triangles?
+
No, these ratios are specific to 30-60-90 triangles. Other triangles with different angles will have different side ratios or require different methods for solving.