5 Key Facts: 30-60-90 Triangle Mastery Guide
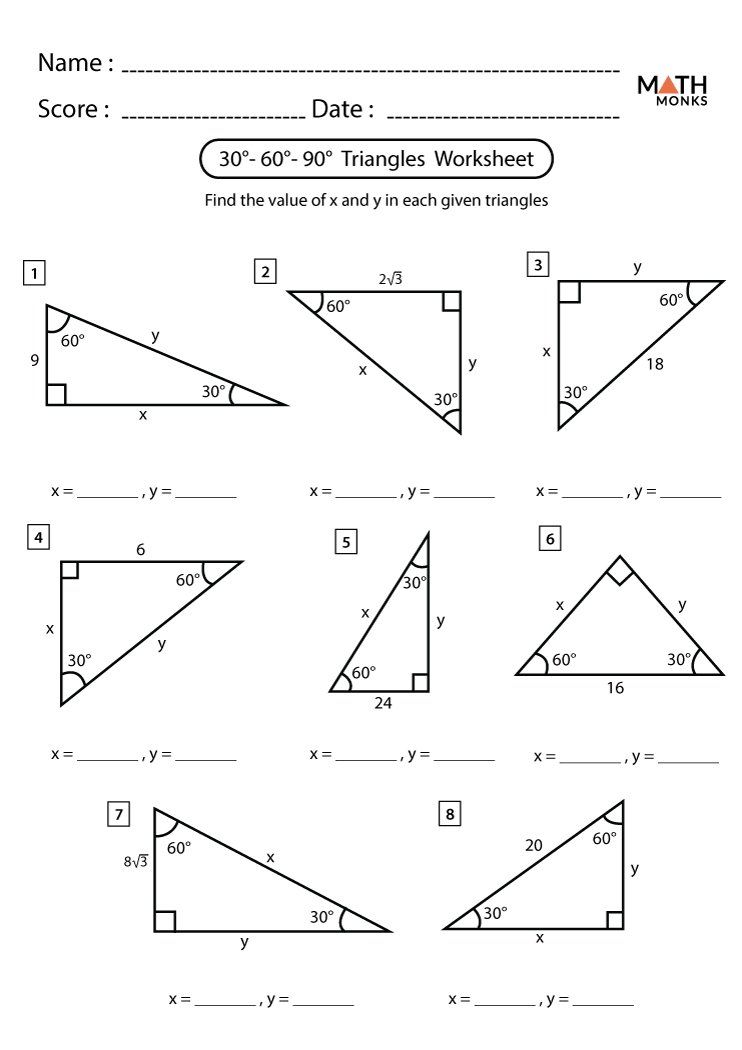
In the world of geometry, certain shapes stand out not only for their aesthetic appeal but also for their unique properties and practical applications. Among these, the 30-60-90 triangle is particularly notable. Known for its distinct angles and side relationships, mastering this triangle can unlock numerous problem-solving skills and enhance your understanding of trigonometric functions. Here, we delve into five key facts that will help you master the 30-60-90 triangle, providing you with the foundational knowledge to excel in both academic and real-world settings.
What is a 30-60-90 Triangle?
Before diving into the intricacies, let’s establish what a 30-60-90 triangle is. This special type of right triangle:
- Has angles measuring 30 degrees, 60 degrees, and 90 degrees.
- The side opposite the 30-degree angle (the shortest side) is half the length of the hypotenuse.
- The side opposite the 60-degree angle is (\sqrt{3}) times the length of the shortest side.

Understanding these ratios is crucial for solving related geometric problems effectively.
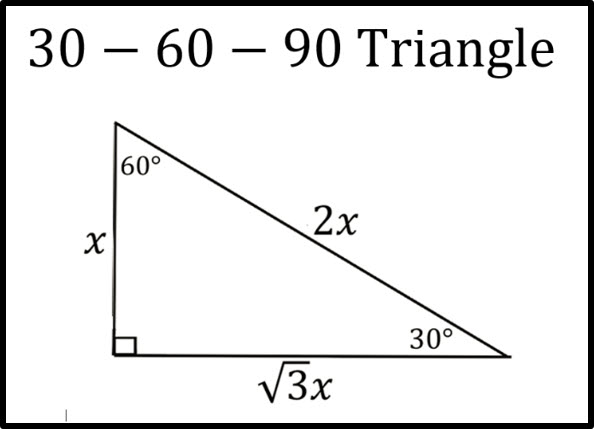
Key Fact 1: Side Lengths and Ratio

The most fundamental property of the 30-60-90 triangle involves its side lengths:
- The hypotenuse is twice the length of the shortest side.
- The longer leg (opposite the 60-degree angle) is (\sqrt{3}) times the shorter leg.
| Angle | Side Length |
|---|---|
| 30° | x |
| 60° | x√3 |
| 90° | 2x |
💡 Note: Knowing these ratios can save time in calculations, especially when dealing with complex problems.
Key Fact 2: Trigonometric Functions
In a 30-60-90 triangle, the trigonometric functions for each angle have fixed values:
- Sine of 30° = Cosine of 60° = 1⁄2
- Sine of 60° = Cosine of 30° = √3/2
- Tangent of 30° = √3/3, Tangent of 60° = √3
These fixed values make it particularly useful for quick reference in trigonometry.
Key Fact 3: Application in Real-Life Problems

Mastering the 30-60-90 triangle has numerous practical applications:
- Architecture: Calculating roof pitches or design angles for staircases.
- Engineering: Understanding stress distribution in triangular supports.
- Navigation: Determining bearings in maritime or aviation contexts.
The precision and simplicity of the 30-60-90 triangle’s ratios facilitate accurate measurements and design.
Key Fact 4: Constructing a 30-60-90 Triangle

One of the easiest ways to construct this triangle is:
- Draw an equilateral triangle with all sides equal.
- Identify the midpoint of one of its sides.
- Draw a perpendicular line from this midpoint to the opposite vertex.
- This perpendicular bisector will split the equilateral triangle into two 30-60-90 triangles.
This method visually reinforces the ratio properties of the 30-60-90 triangle.
Key Fact 5: Proofs and Higher Mathematics

The 30-60-90 triangle plays a significant role in:
- Pythagorean Theorem proofs
- Properties of sine, cosine, and tangent
- Trigonometric identities
It is often used to introduce students to more complex trigonometric identities and functions.
In sum, understanding the 30-60-90 triangle not only simplifies solving geometric problems but also enriches one's grasp of mathematical principles. From quick calculations in geometry to real-world applications, this triangle's mastery is a cornerstone of mathematical competence. Its fixed ratios and angles offer a unique blend of predictability and utility, making it an invaluable tool for students, engineers, architects, and mathematicians alike. Whether you're designing, calculating, or simply exploring the beauty of shapes, the 30-60-90 triangle provides a clear path to accuracy and understanding.
Can a 30-60-90 triangle have sides of any length?
+
The 30-60-90 triangle’s sides are always in a specific ratio, but this ratio can be scaled. The hypotenuse must always be twice the length of the shortest side, with the longer leg being (\sqrt{3}) times the shorter leg. Thus, while the absolute length can vary, the ratio remains constant.
How does understanding 30-60-90 triangles help with trigonometry?
+
Knowing the fixed values for sine, cosine, and tangent in a 30-60-90 triangle allows for quicker reference and problem solving in trigonometric functions, especially when you’re working with these angles or their multiples.
What are some common mistakes when dealing with 30-60-90 triangles?

+
Common errors include misapplying the side length ratio, confusing the angles, or miscalculating trigonometric values. It’s essential to remember that the hypotenuse is the longest side and that the ratios are fixed.