30-60-90 Triangle Answers: Quick Worksheet Solutions

Introduction to the 30-60-90 Triangle

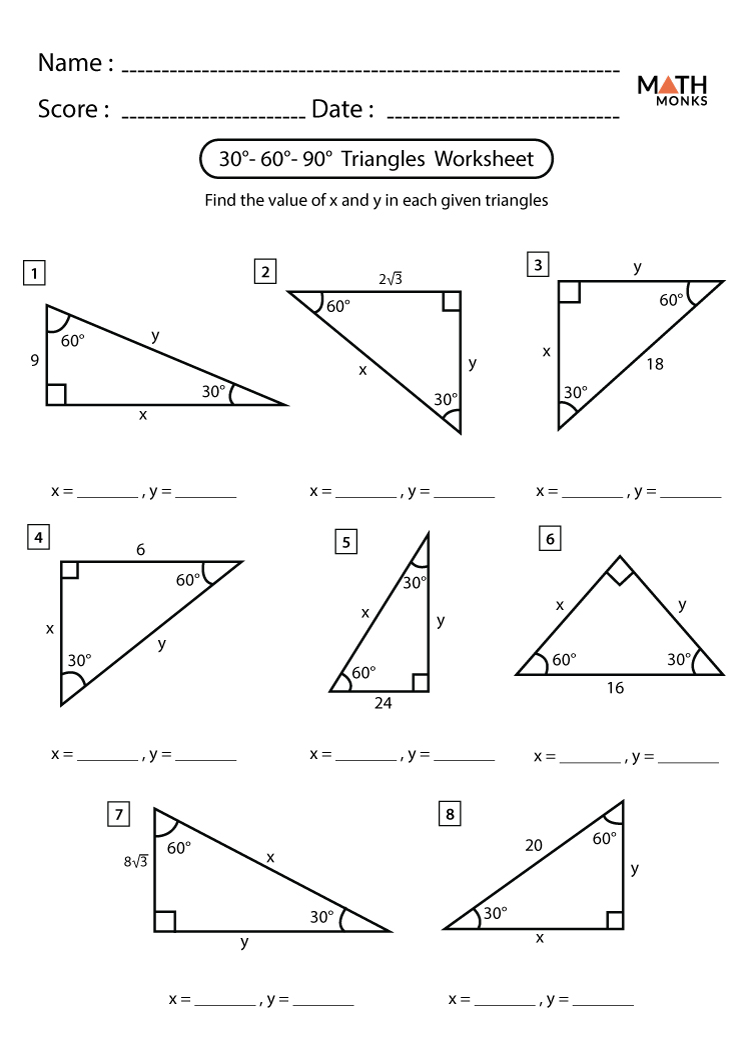
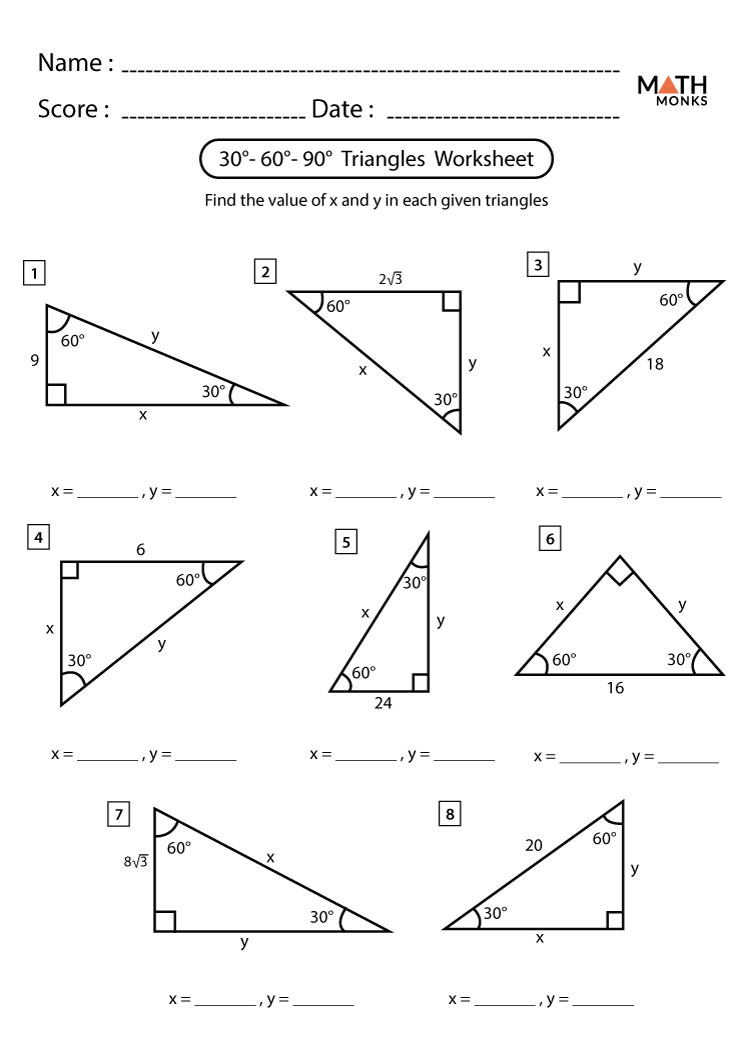
The 30-60-90 triangle is a special type of right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. This unique triangle has properties that make it a frequent subject in geometry and trigonometry lessons due to the simplicity in its side length ratios. Understanding these triangles can not only help you with geometry problems but also assist in various fields like engineering and architecture where precise measurements are crucial. Let’s dive into what makes this triangle special and how you can solve problems involving it quickly and accurately.
Properties of a 30-60-90 Triangle

A 30-60-90 triangle follows specific rules regarding its sides:
- Shortest side (opposite 30°): This side is always half the hypotenuse.
- Medium side (opposite 60°): This side is the shortest side multiplied by the square root of 3.
- Longest side (Hypotenuse, opposite 90°): This side is twice the length of the shortest side.
Here’s how these sides relate:
- Shortest side: x
- Medium side: x * √3
- Hypotenuse: 2x
🔍 Note: The constant ratio of these sides allows for easy calculation once you know one side's length.
Solving for the Sides

If you are given one side of a 30-60-90 triangle, you can determine the other sides by applying the above ratios. Here’s how:
- Given the Shortest Side: Multiply by 2 for the hypotenuse and by √3 for the medium side.
- Given the Hypotenuse: Divide by 2 for the shortest side, then multiply the shortest side by √3 for the medium side.
- Given the Medium Side: Divide by √3 to find the shortest side, then multiply the shortest side by 2 for the hypotenuse.
Example 1: Finding All Sides

Suppose the shortest side is 3 units:
- Shortest Side = 3 units
- Medium Side = 3 * √3 ≈ 5.2 units
- Hypotenuse = 3 * 2 = 6 units
🎓 Note: Always keep an eye on the units, ensuring consistency in your calculations.
Example 2: Using Hypotenuse

If the hypotenuse is 8 units:
- Shortest Side = 8/2 = 4 units
- Medium Side = 4 * √3 ≈ 6.93 units
- Hypotenuse = Given (8 units)
Advanced Applications

The 30-60-90 triangle not only simplifies calculations but also has practical applications:
- Surveying: Determining angles and distances on the ground.
- Architecture: Designing roof pitches or staircases with specific angles.
- Navigation: Especially in aviation or maritime for computing bearings.
Trigonometric Functions

The trigonometric ratios (sine, cosine, and tangent) in a 30-60-90 triangle are straightforward:
| Angle | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| 30° | ½ | √3/2 | 1/√3 ≈ 0.577 |
| 60° | √3/2 | ½ | √3 ≈ 1.732 |
| 90° | 1 | 0 | undefined |
✏️ Note: These exact values make 30-60-90 triangles invaluable in trigonometry calculations.
To conclude, understanding the 30-60-90 triangle unlocks a multitude of mathematical and real-world applications. By recognizing the unique proportions and trigonometric relationships, you can quickly solve geometric problems, navigate architectural designs, and apply these principles in various fields requiring precise measurement and calculation.
The simplicity of these relationships offers a foundational understanding of more complex geometries and trigonometry, ensuring that even challenging problems become approachable with practice and application of these concepts.
Why are 30-60-90 triangles considered special?
+
30-60-90 triangles are special because they have fixed ratio relationships between their sides, which simplifies solving problems involving them. This specific ratio helps in various fields where precise measurements are needed.
What are some common mistakes when working with 30-60-90 triangles?

+
One common mistake is confusing the ratios of the sides or neglecting to use the right units consistently throughout the problem. Another frequent error is applying the Pythagorean theorem instead of using the known ratios directly.
Can 30-60-90 triangles help with understanding trigonometry?
+
Yes, they can! The exact values of sine, cosine, and tangent for 30 and 60 degrees provide foundational knowledge for trigonometry, making it easier to work with angles and sides in more complex problems.



