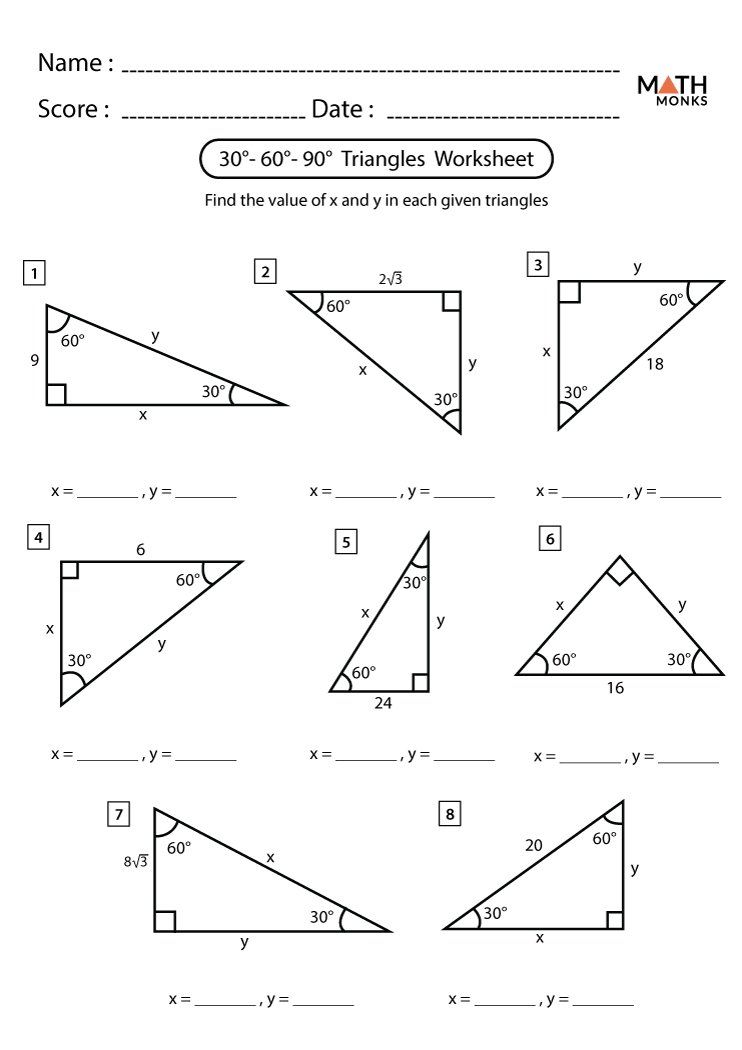
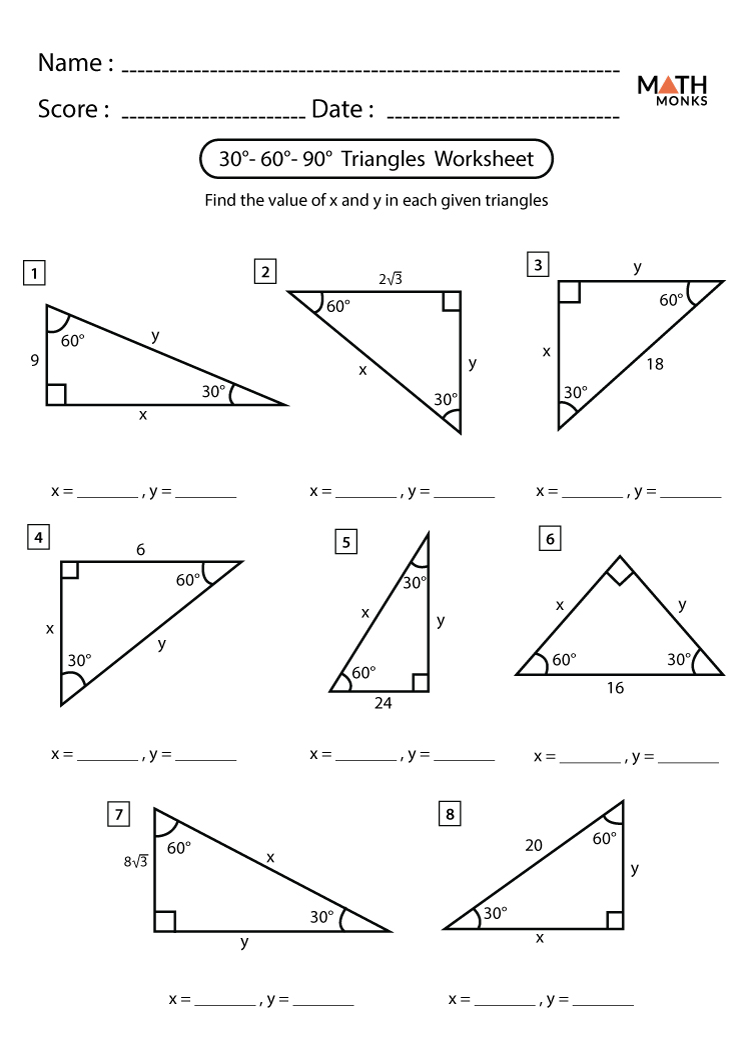
30-60-90 Triangle Worksheet: 5 Quick Solve Methods

30-60-90 triangles are a specific type of right triangle with a unique ratio between the sides. Mastering the 30-60-90 triangle is not only key for high school geometry students but also useful for anyone delving into trigonometry, engineering, or architecture. Here's how you can quickly solve problems involving these triangles with five different methods, each focusing on a different aspect of the triangle's properties.
The Basic Properties of a 30-60-90 Triangle
- Shortest Side (opposite 30°): The side opposite to the 30-degree angle is the shortest, and it’s half the length of the hypotenuse.
- Middle Side (opposite 60°): This side is √3 times the length of the shortest side.
- Hypotenuse: The hypotenuse is twice the length of the shortest side.
The relationship between these sides is elegantly expressed in a simple ratio: 1 : √3 : 2.
Method 1: Using the Ratios

The most straightforward method to solve 30-60-90 triangles is by directly applying the ratio:
- Given the shortest side: If you know the length of the side opposite the 30-degree angle, multiply it by 2 to get the hypotenuse and by √3 to get the other leg.
- Given the hypotenuse: Divide it by 2 to find the shortest side, then multiply the shortest side by √3 for the other side.
- Given the middle side: Divide it by √3 to find the shortest side, then multiply the shortest side by 2 for the hypotenuse.
✏️ Note: Always use the correct decimal approximation for √3 when performing calculations by hand. √3 ≈ 1.732.
Method 2: Using the Pythagorean Theorem

While the ratio method is quicker, you can also use the Pythagorean theorem to find missing sides:
- Hypotenuse: (Shortest side)2 + (Middle side)2 = (Hypotenuse)2
- Shortest Side: Use the theorem if you know the hypotenuse and one other side.
- Middle Side: Similar application as above, substituting known values.
✏️ Note: Remember, this method is particularly useful when ratios are not immediately evident, or if you need a sanity check for your ratio-based calculations.
Method 3: Trig Ratios

Trigonometric functions provide another avenue for solving 30-60-90 triangles:
- Sine: sin(30°) = 0.5, sin(60°) = √3/2
- Cosine: cos(30°) = √3/2, cos(60°) = 0.5
- Tangent: tan(30°) = 1/√3, tan(60°) = √3
Using these ratios can be particularly helpful when dealing with angles or when you need to calculate the length of a side relative to an angle.
Method 4: Similarity

30-60-90 triangles are similar to each other; thus, if you have two triangles with the same angles, they are similar by AA similarity criterion. This means:
- Set up ratios of corresponding sides.
- Solve for unknown sides using these ratios.
This approach is beneficial when dealing with multiple triangles or when indirect methods are needed for solving.
Method 5: Using Coordinates and Distance Formula
If you place the triangle in a coordinate system:
- Set Origin: Place the vertex at (0, 0).
- Shortest Side on X-axis: Extend along the x-axis.
- Use Distance Formula: Calculate distances between known points to find missing sides.
✏️ Note: This method, though not typically taught for basic triangles, can provide insight into the geometric relationships in a broader mathematical context.
By understanding these five quick solve methods, you're equipped to tackle any problem involving 30-60-90 triangles. Each approach has its strengths, making it suitable for different scenarios or problem types. Whether you're in the classroom, preparing for an exam, or working on a design project, these methods ensure you have the tools necessary to navigate through triangle-based problems efficiently. The ratios and properties of these triangles have stood the test of time, proving their practicality and elegance in the world of geometry and beyond.
What is a 30-60-90 triangle?

+
A 30-60-90 triangle is a special right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The sides of this triangle are in a ratio of 1:√3:2.
How do you use the Pythagorean theorem in a 30-60-90 triangle?

+
You can use the Pythagorean theorem to find any missing side if you know the length of any two sides of the triangle. It can confirm or check your calculations made using the known ratio.
Why are trigonometric ratios useful for 30-60-90 triangles?

+
Trigonometric ratios provide a shortcut to finding the length of sides relative to known angles, which can be faster than using the Pythagorean theorem or direct ratio application, especially in complex problems or when dealing with angles.
Can 30-60-90 triangles be similar to other triangles?

+
Yes, all 30-60-90 triangles are similar to each other because they have the same angles. This allows for setting up ratios to solve for unknown sides.
When would you use the coordinate method for a 30-60-90 triangle?

+
This method might be used when working with geometric proofs or when you need to understand the placement of points and distances within a coordinate system for a more comprehensive understanding of the triangle’s properties.