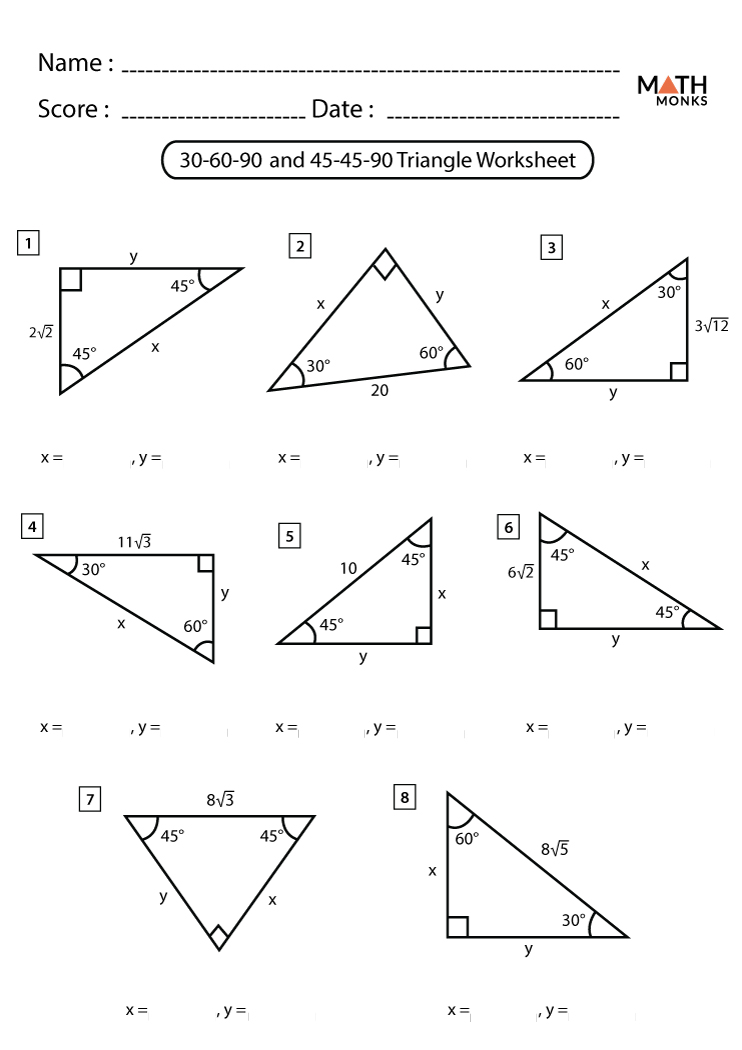
Mastering 30-60-90 & 45-45-90 Triangles: Engaging Worksheet

Welcome to the world of triangles, where geometry gets a little more interesting with the introduction of the 30-60-90 and 45-45-90 triangles. These special right triangles have unique properties that make solving for their sides and angles straightforward and efficient. Whether you're a student learning geometry or a professional who needs a quick review, this worksheet will guide you through the essential concepts and practical applications of these triangles.
The Basics of Special Right Triangles

Before diving into the worksheets, let’s get a fundamental understanding of what makes 30-60-90 and 45-45-90 triangles so special:
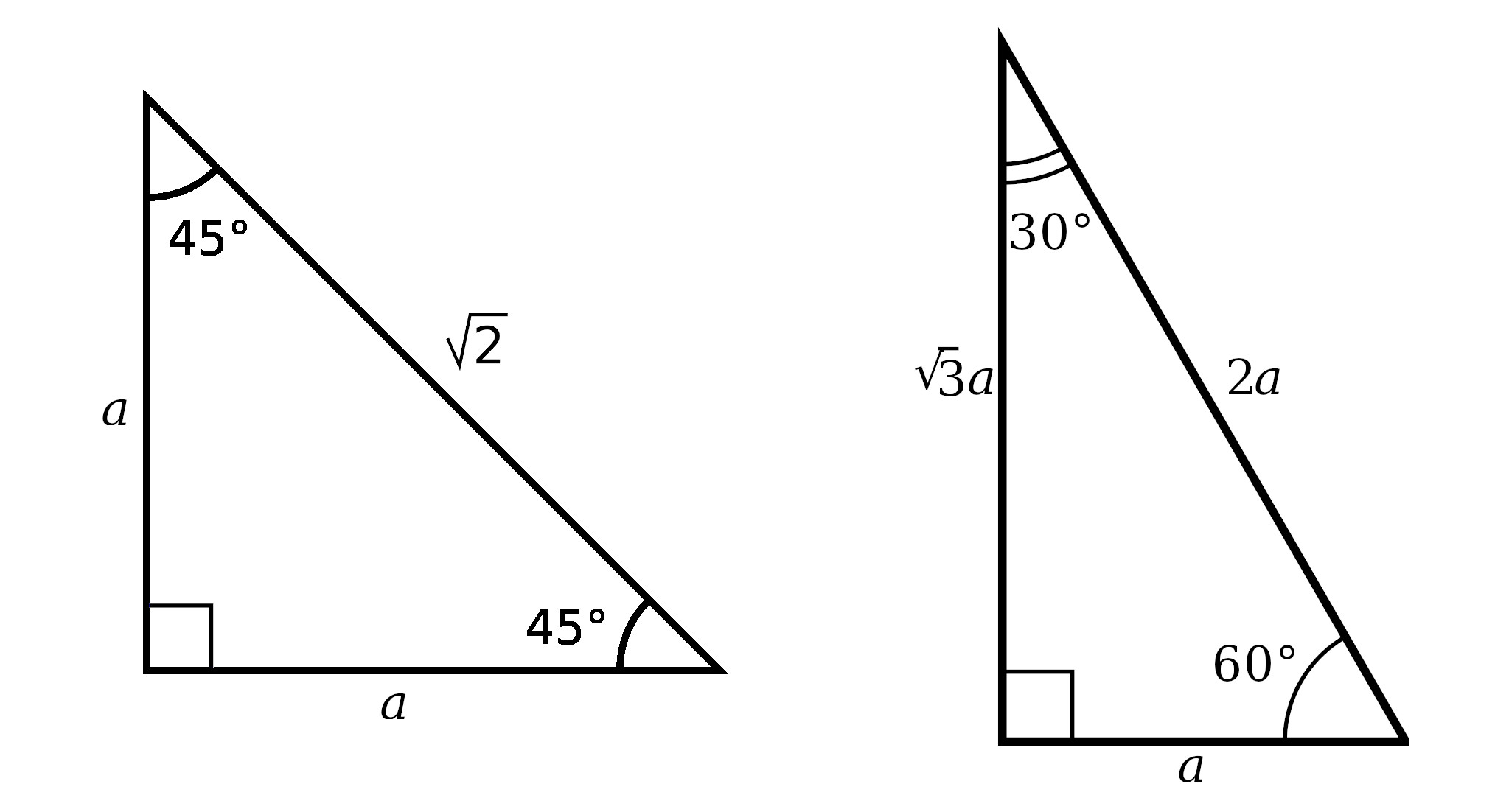
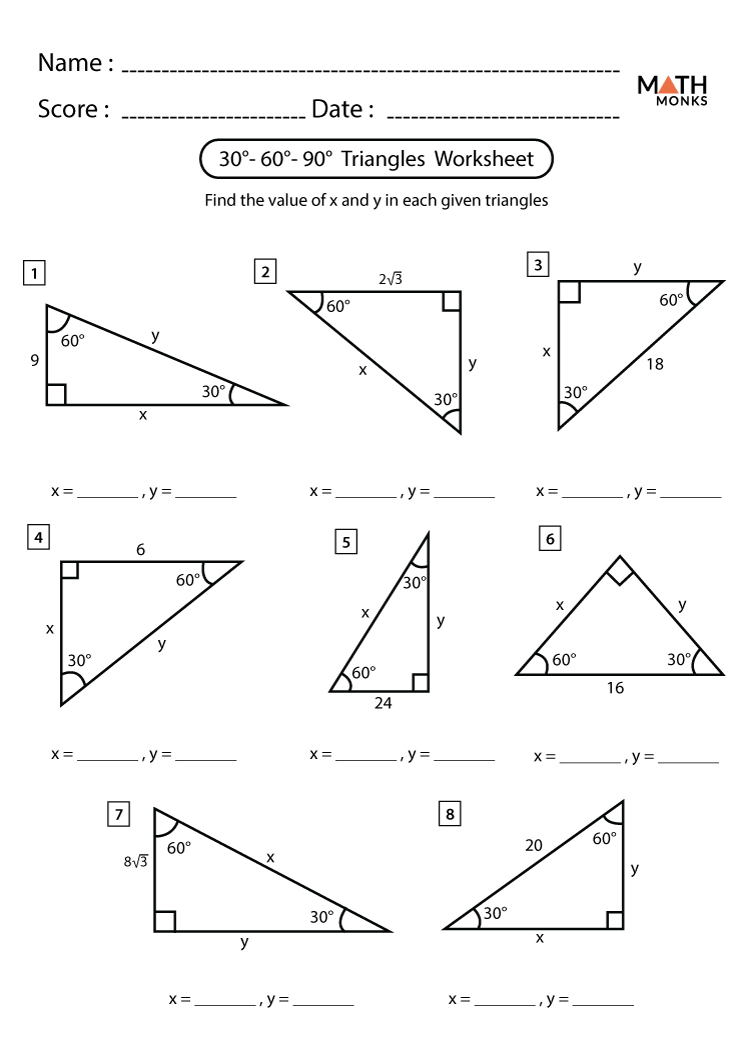
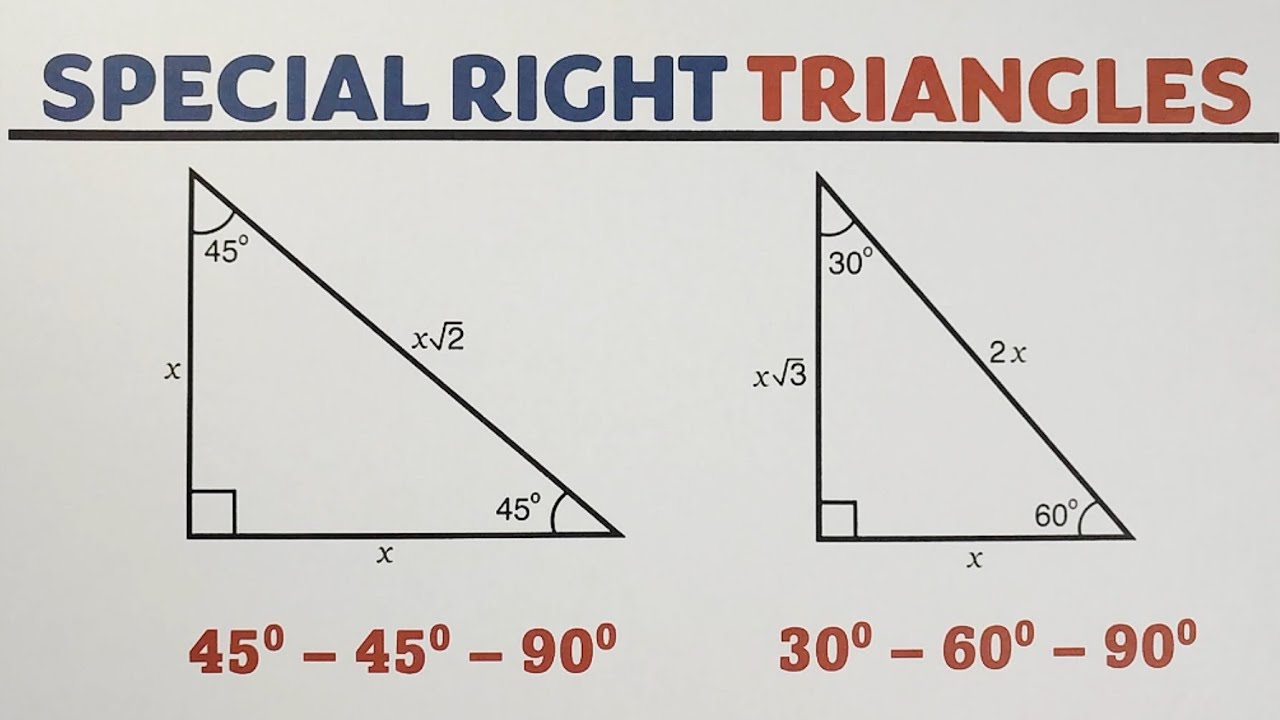
- 30-60-90 Triangle: This triangle has angles of 30°, 60°, and 90°. The ratio of the lengths of its sides opposite these angles is 1 : √3 : 2.
- 45-45-90 Triangle: Known as an isosceles right triangle, where both legs are equal, and the angles are 45°, 45°, and 90°. Here, the ratio of the sides is 1 : 1 : √2.
Worksheet: 30-60-90 Triangles

In this section, we’ll dive into exercises to help you master the 30-60-90 triangle:
| Side Ratio | Side Lengths Example | Angle Ratios |
|---|---|---|
| 1 : √3 : 2 | 3, 3√3, 6 | 30° : 60° : 90° |
| 1 : √3 : 2 | 5, 5√3, 10 | 30° : 60° : 90° |

Example Problems
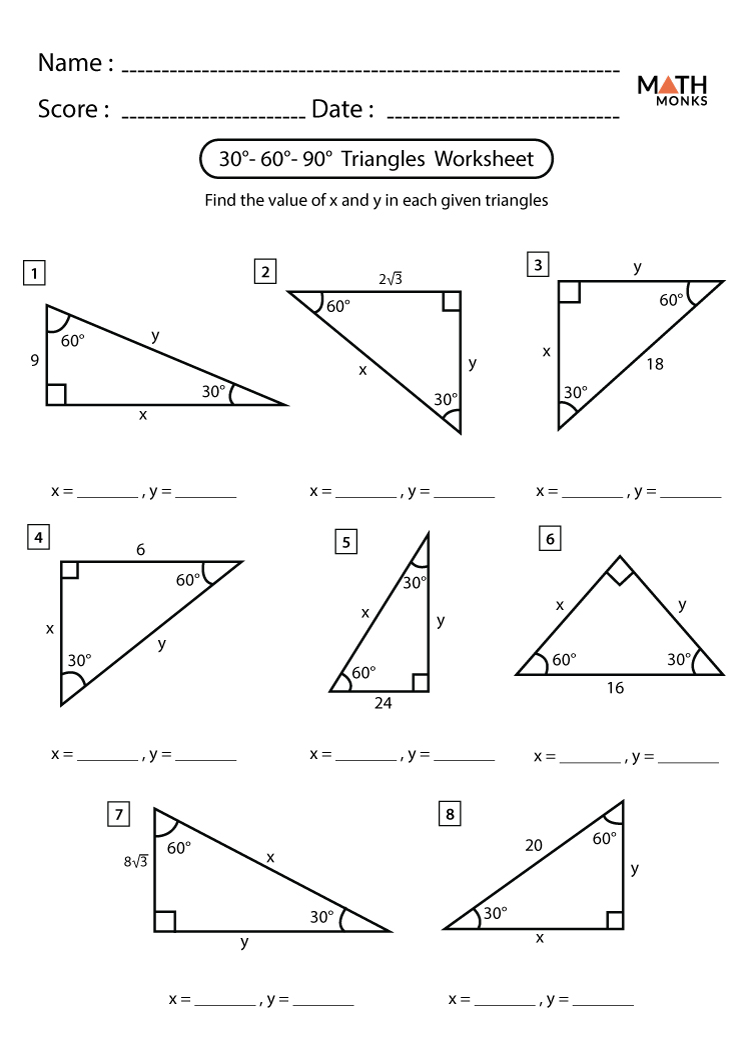
Let’s solve some problems to understand how these ratios work:
- Problem 1: Given the length of the shortest side in a 30-60-90 triangle is 5 units, find the lengths of the other sides.
- The shortest side (opposite the 30° angle) is the base for our ratio, so:
- Hypotenuse: 5 x 2 = 10 units
- The side opposite to the 60° angle: 5 x √3 = 5√3 units
- Problem 2: If the hypotenuse of a 30-60-90 triangle is 12 units, calculate the lengths of the remaining sides.
- The hypotenuse is our starting point:
- The shortest side: 12 / 2 = 6 units
- The side opposite to the 60° angle: 6 x √3 = 6√3 units
Application
These ratios are not just for math problems; they have practical applications:
- Architecture: Calculating roof slopes or designing staircases.
- Engineering: Determining force vectors or structural stability.
📝 Note: Remember to check your work by ensuring the Pythagorean theorem (a² + b² = c²) holds true for your triangle.
Worksheet: 45-45-90 Triangles
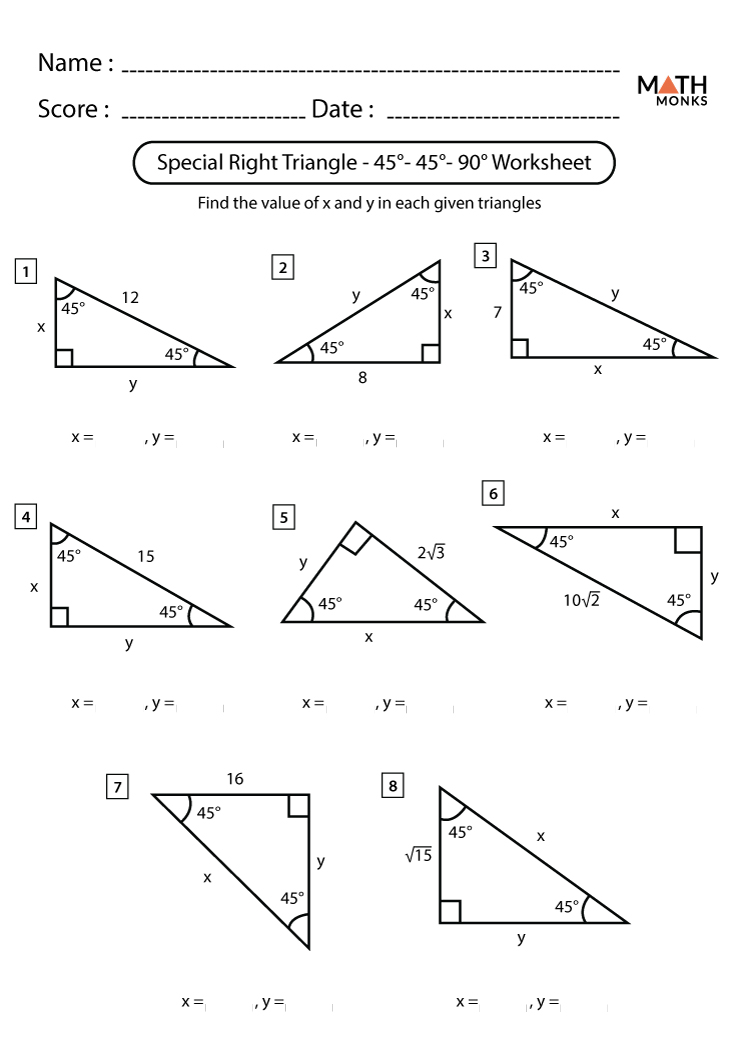
Here, we explore the properties of the 45-45-90 triangle:
| Side Ratio | Side Lengths Example | Angle Ratios |
|---|---|---|
| 1 : 1 : √2 | 4, 4, 4√2 | 45° : 45° : 90° |
| 1 : 1 : √2 | 6, 6, 6√2 | 45° : 45° : 90° |
Example Problems

Now, let’s solve problems to get a grip on this triangle:
- Problem 1: If one leg of a 45-45-90 triangle is 8 units, what are the lengths of the other sides?
- The other leg will also be 8 units.
- The hypotenuse will be 8 x √2 = 8√2 units.
- Problem 2: Find the legs of a 45-45-90 triangle if its hypotenuse is 10√2 units.
- Since the hypotenuse is √2 times the length of one leg, dividing by √2:
- Legs: 10√2 / √2 = 10 units each
Application

This triangle’s properties are useful in various fields:
- Art and Design: For creating symmetrical compositions or designing pathways.
- Surveying: When leveling a plot of land or determining slopes.
In Summation

Exploring the 30-60-90 and 45-45-90 triangles not only deepens your understanding of geometry but also equips you with tools for problem-solving in diverse applications. From practical applications in architecture to the simplicity in calculation, these triangles are not just shapes but powerful geometric constructs.
What makes 30-60-90 and 45-45-90 triangles special?
+
These triangles have predictable side ratios, making them useful for quick calculations. The 30-60-90 triangle has sides in the ratio 1 : √3 : 2, while the 45-45-90 triangle’s ratio is 1 : 1 : √2.
How do I use the side ratios to find missing lengths?
+
Identify the known side length and use the ratio to calculate the others. For example, in a 30-60-90 triangle, if you know the shortest side, multiply by √3 for the next side and by 2 for the hypotenuse.
Can these triangles be used in real-life scenarios?
+
Absolutely, from engineering for force calculations to design and construction for creating balanced structures, these triangles provide a solid foundation for various applications.