5 Must-Know Answers for Parallel Lines Worksheet

Geometry can be a fascinating subject, especially when diving into the realm of parallel lines and their properties. Whether you're a student tackling geometry homework or an enthusiast curious about this mathematical area, this blog post will elucidate some of the trickiest concepts related to parallel lines worksheets. Here, we'll address 5 Must-Know Answers that are crucial for understanding and mastering these exercises.
Understanding the Basics of Parallel Lines

Before we delve into the specifics, let’s ensure we have a firm grasp of the basics:
- Parallel Lines: Two lines on the same plane that do not intersect or cross each other are termed as parallel. In geometry, these are often denoted with the symbol “||”.
- Transversal: A line that cuts through two or more parallel lines is called a transversal. This interaction creates several angles which are key to solving parallel lines problems.

🔍 Note: Understanding the basic terminology is key when working through geometry problems, as these terms will appear in problems and their solutions.
The Angles Formed by Parallel Lines and a Transversal

When a transversal intersects two parallel lines, eight angles are formed. Here’s a breakdown:
- Corresponding Angles: These angles are in the same position at each intersection; they are congruent.
- Alternate Interior Angles: These pairs lie on opposite sides of the transversal but inside the parallel lines; they are also congruent.
- Alternate Exterior Angles: They are similar to alternate interior angles but lie on the outside of the parallel lines; they are congruent as well.
- Consecutive Interior Angles or Same-Side Interior Angles: These lie on the same side of the transversal and are supplementary (sum up to 180°).
- Vertical Angles: Directly opposite each other, these angles are congruent.
📘 Note: The properties of these angles become the backbone for solving complex geometry problems involving parallel lines.
Question 1: How to Identify Corresponding Angles?
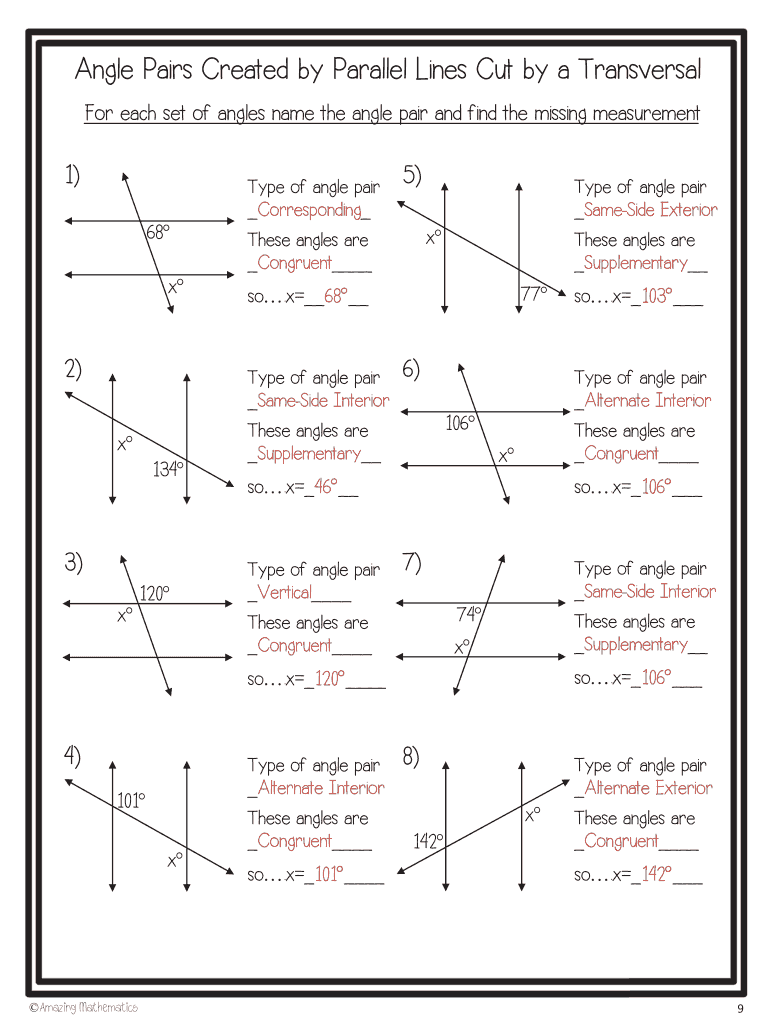
Corresponding angles can be identified by their position relative to the transversal. Here’s how:
- Look for angles that are on the same side of the transversal, with one angle being at an intersection point above and the other below the parallel lines.
- They will be congruent if the lines are parallel.
| Angle Type | Position | Congruence |
|---|---|---|
| Corresponding | Same side of transversal, one above, one below parallel lines | Yes |
| Alternate Interior | Opposite side of transversal, inside the parallel lines | Yes |
| Consecutive Interior | Same side of transversal, inside the parallel lines | No (Supplementary) |

Question 2: Calculating Angle Measurements Using Parallel Lines

Solving for angles in parallel lines setups requires understanding the relationships between the angles. Here’s a step-by-step approach:
- Identify the type of angle (e.g., corresponding, alternate interior, etc.).
- Use the properties of the angles to set up an equation. For instance:
- If you have two corresponding angles, they are congruent. So if one angle is 70°, the corresponding angle will also be 70°.
- If you have alternate interior angles, they too are congruent. Thus, if one angle is 45°, the other will be 45°.
- If you have consecutive interior angles, they are supplementary. If one angle is 110°, the other will be 180° - 110° = 70°.
- Solve the equation to find the unknown angle(s).
🔍 Note: Remember, angles formed by parallel lines can often be solved using algebra, by setting up equations and solving for the unknown.
Question 3: Prove Parallel Lines
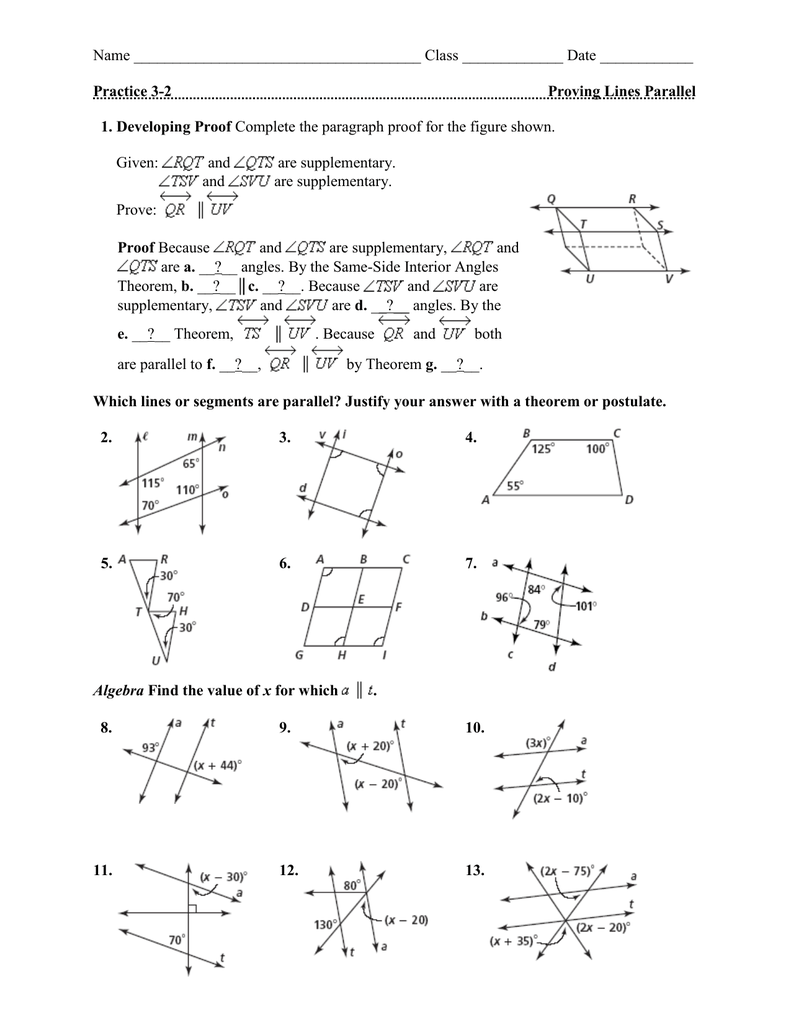
Often in geometry, you need to prove that two lines are parallel. Here are the ways to prove parallel lines:
- Converse of Corresponding Angles Postulate: If corresponding angles are congruent, the lines are parallel.
- Converse of Alternate Interior Angles Theorem: If alternate interior angles are congruent, the lines are parallel.
- Converse of Consecutive Interior Angles Theorem: If consecutive interior angles are supplementary, the lines are parallel.
- Slopes of Lines: Two lines are parallel if they have the same slope. If you can calculate the slopes of two lines and find them to be equal, they are parallel.
📘 Note: Proving lines are parallel requires not just understanding these theorems but also the ability to apply them correctly in geometric contexts.
Question 4: When Does the Parallel Postulate Matter?

The Parallel Postulate, also known as Euclid’s Fifth Postulate, is fundamental to Euclidean geometry. Here’s why it matters:
- It defines the uniqueness of parallel lines through a point not on the line.
- It underpins the sum of angles in a triangle being 180°.
- It is crucial in the proof of many theorems involving parallel lines, like the one proving the area of a parallelogram or the properties of similar triangles.
Question 5: What about Non-Euclidean Geometry?

While this post focuses on Euclidean geometry, there’s more to know:
- In spherical geometry, there are no parallel lines; all lines on a sphere intersect.
- In hyperbolic geometry, there can be multiple lines through a point not on the line that do not intersect the given line.
- Understanding non-Euclidean geometries broadens our perspective on parallel lines and their behavior in different spatial environments.
🔍 Note: Non-Euclidean geometries like spherical and hyperbolic geometry offer fascinating insights into how space can behave differently from what we’re used to in our everyday experiences.
In this in-depth look at parallel lines worksheets, we've covered the essential answers to questions often asked by those looking to master these problems. From understanding the basic principles to identifying and calculating angles, proving parallel lines, recognizing the significance of the Parallel Postulate, and briefly exploring non-Euclidean geometries, the knowledge base you've built here is strong. Keep practicing, and don't hesitate to explore deeper into each of these areas. Remember, every angle, every line, and every postulate is a piece of the larger geometric puzzle.
What are the angles formed by parallel lines and a transversal?

+
When a transversal intersects two parallel lines, eight angles are formed: corresponding angles, alternate interior angles, alternate exterior angles, consecutive interior angles, and vertical angles.
How do you prove that two lines are parallel?

+
You can prove lines are parallel by showing that corresponding angles are congruent, alternate interior angles are congruent, consecutive interior angles are supplementary, or by comparing their slopes.
Why is the Parallel Postulate important?

+
The Parallel Postulate, or Euclid’s Fifth Postulate, defines the uniqueness of parallel lines through a point not on the line and underpins many theorems involving parallel lines.
What’s the difference between Euclidean and Non-Euclidean geometries?
+
Euclidean geometry assumes a flat, infinite plane with parallel lines never intersecting, whereas Non-Euclidean geometries like spherical or hyperbolic have different rules for parallel lines and their behavior.
Can angles between parallel lines ever be 90 degrees?

+
Yes, when two parallel lines are cut by a perpendicular transversal, all corresponding angles will be 90 degrees, making the lines perpendicular to the transversal.