2 Step Word Problems: 5 Tips for Quick Solving
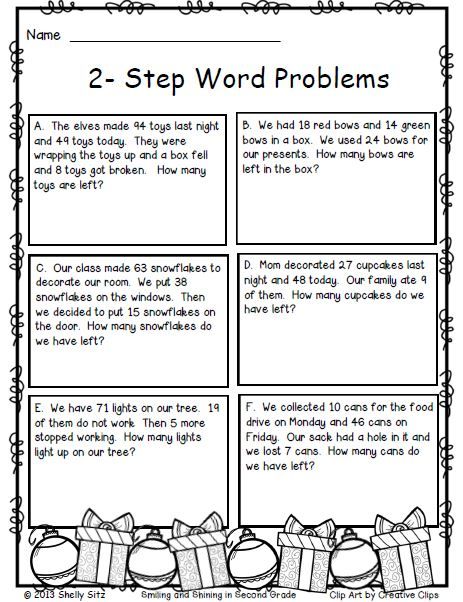
Understanding the Basics of Two-Step Word Problems

Two-step word problems are common in mathematics education, particularly from elementary to middle school levels. These problems require students to break down a complex scenario into simpler, manageable steps before solving. This ability to deconstruct and solve step-by-step is not only crucial for mathematical proficiency but also for logical reasoning in real-life situations.
Why Two-Step Word Problems Are Important

- Critical Thinking: These problems foster the development of critical thinking skills by requiring students to understand what the problem asks, how to approach it, and how to organize their thoughts systematically.
- Practical Skills: In everyday life, most decisions require a series of logical steps, making two-step word problems an excellent tool for preparing students for real-world problem-solving.
- Mathematical Foundations: They reinforce foundational concepts like addition, subtraction, multiplication, and division within a problem-solving context, making these operations more meaningful.
Tip 1: Identify the Two Steps
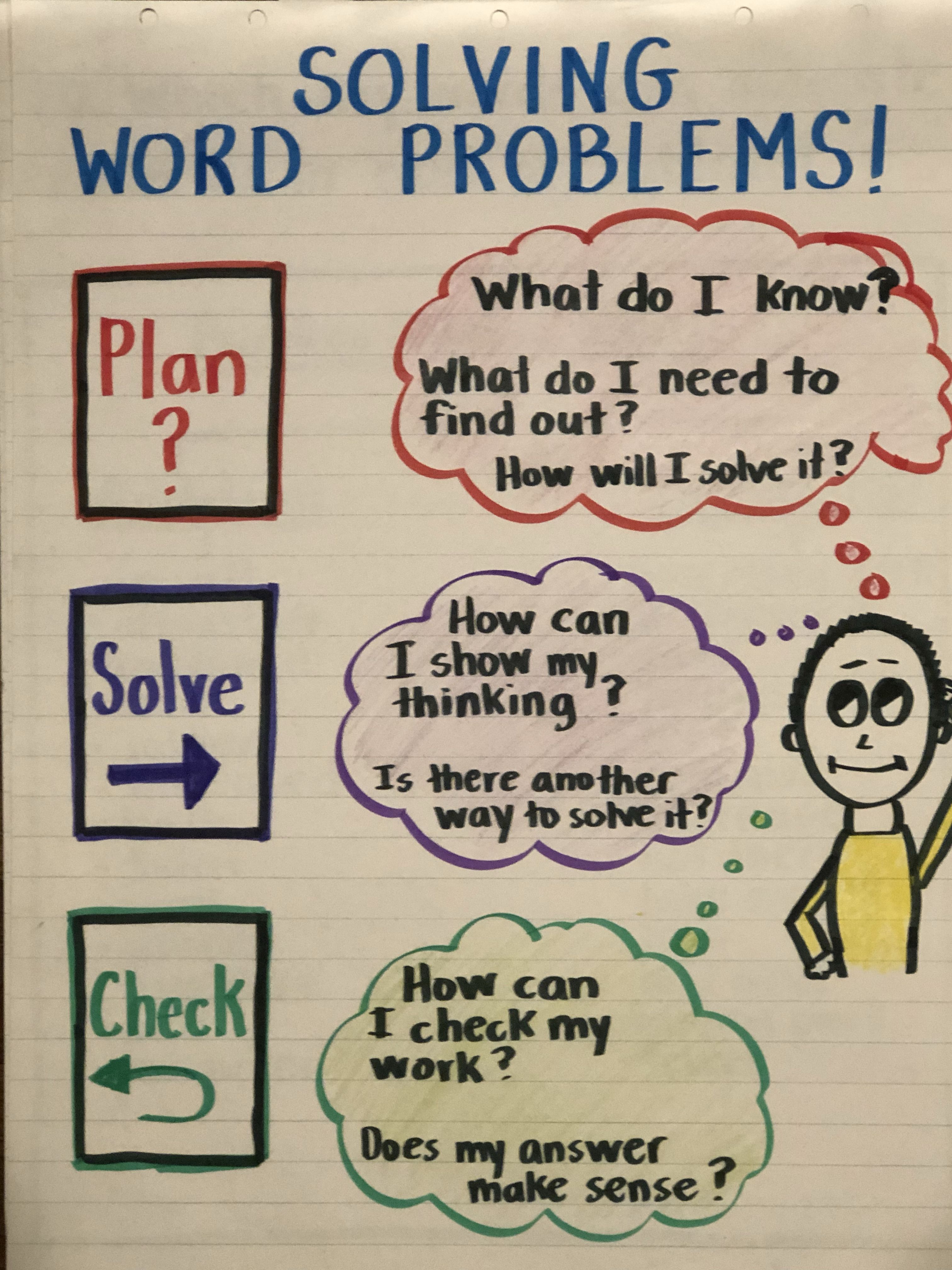
The first tip for solving two-step word problems efficiently is to clearly identify the two distinct steps required to solve the problem. Here’s how you can do it:
- Read the Problem Carefully: Understand what information is given and what is being asked.
- Break Down the Information: Distinguish between the initial information (often describing a situation) and the subsequent information (which leads to the final question).
- Mark the Steps: Physically or mentally note the points where you need to apply different operations or calculations.
For example, consider the problem: “John bought 12 apples for $24. If he gives 3 apples to his friend, how much did he spend on the remaining apples?” Here, the first step is calculating the cost per apple (24⁄12), and the second is calculating the total cost for 9 apples (price per apple * 9).
Tip 2: Use Drawings or Diagrams

Sometimes, the complexity of word problems can be reduced by visualizing the scenario:
- Visual Aid: Sketch out a rough drawing or diagram that represents the situation described in the problem.
- Clarify Quantities: Label quantities on the diagram to make it easier to see the relationships between different parts of the problem.
- Track Changes: Use arrows or other symbols to show how quantities change as you work through the problem.
| Scenario | Step 1 | Step 2 |
|---|---|---|
| John with 12 apples | Calculate price per apple | Calculate price for remaining 9 apples |

Tip 3: Translate Words to Math

Mathematics has its own language. Here’s how you can convert wordy problems into solvable equations:
- Identify Key Terms: Words like “times”, “divide”, “per”, “each”, “more than”, “less than” should be translated into mathematical symbols like ×, ÷, -, +, etc.
- Formulate Equations: Using the key terms, write down the equations that reflect the steps in the problem.
- Organize Steps: Arrange the steps logically from first to last, ensuring you are addressing the problem in order.
🔍 Note: It’s often helpful to use variables as placeholders to make the translation from words to math more straightforward.
Tip 4: Work Backwards
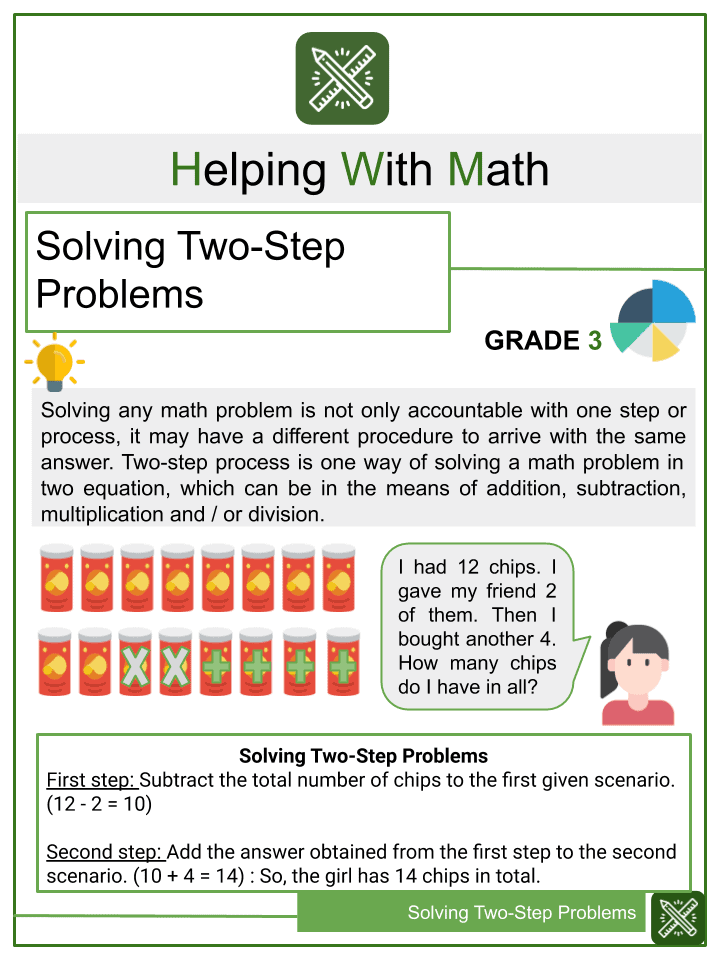
Not all problems require you to work forward. Here’s how to approach problems from the end:
- Determine the End Goal: Know what the problem is asking for first.
- Step Back: Identify what information or calculation would lead to that goal.
- Repeat: Keep stepping backward until you have the initial conditions of the problem.
This method is particularly useful for problems where you need to find an unknown quantity given the result of an equation.
Tip 5: Check Your Work

Finally, always check your work to ensure accuracy:
- Re-read the Problem: Ensure your solution makes sense in the context of the original problem.
- Unit Analysis: Check if your answer has the right units, which can prevent common calculation errors.
- Verification: Sometimes working backward from your answer to the known conditions can verify your solution.
Remember, even the smallest oversight can lead to an incorrect answer, so this step is crucial.
In closing, mastering two-step word problems involves not only understanding the mathematical concepts but also developing a strategic approach to problem-solving. By clearly identifying steps, visualizing the problem, translating words into math, considering working backward, and always checking your work, students can enhance their ability to solve these problems quickly and accurately. These skills will not only serve them well in academics but also in practical, everyday situations where logical analysis and decision-making are required.
How do I know if a word problem is two-step?

+
A problem is likely two-step if it involves calculating or determining intermediate information before you can solve for the final answer. Look for cues like “then” or multiple questions within one problem.
Can these tips help with more complex problems?

+
Absolutely. The principles of breaking down complex problems into smaller, manageable steps, using visual aids, translating into math, and verifying work can apply to problems with many steps or even abstract mathematical puzzles.
Why is visualization important for word problems?

+
Visualization helps students understand the context of the problem, making it easier to break down the information into steps. It also makes the problem less abstract, reducing the cognitive load and facilitating problem-solving.