12.2 Arcs and Chords Worksheet Solutions Unlocked

If you're diving into the world of geometry, understanding arcs and chords in circles can be both intriguing and complex. Let's explore the key concepts and dive into some worksheet solutions to solidify our understanding.
Understanding Arcs and Chords

Arcs: An arc is a portion of the circumference of a circle. There are two types of arcs:
- Major Arc: The longer of the two arcs between two points on a circle, always greater than 180 degrees.
- Minor Arc: The shorter arc between two points on a circle, less than or equal to 180 degrees.
Chords: A chord is a line segment with both endpoints on the circle. Here are some critical relations:
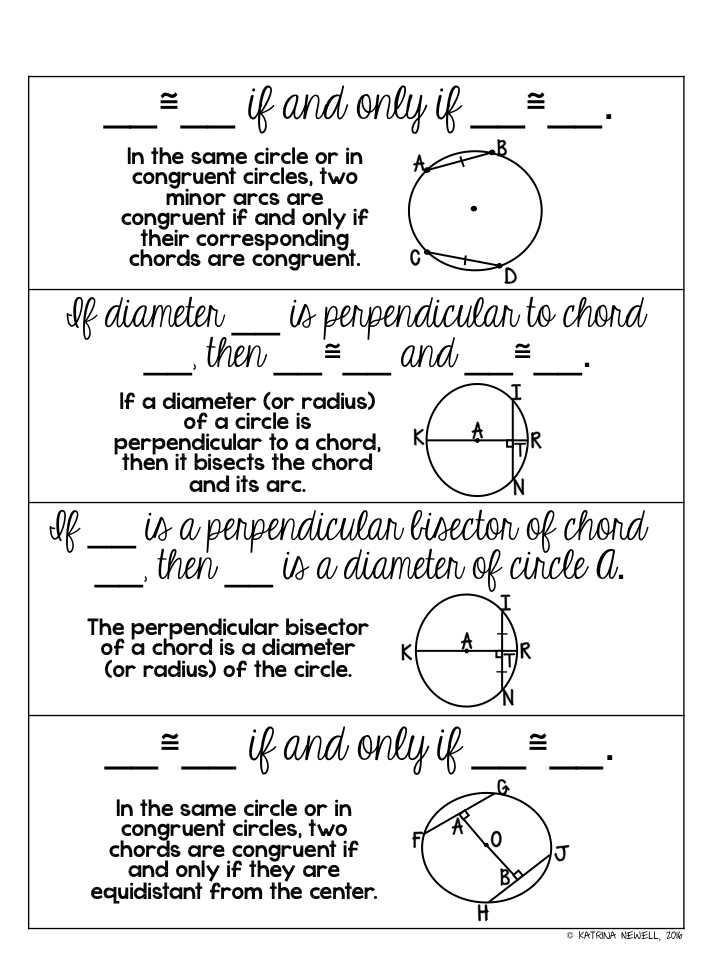
- The diameter is the longest chord in any circle, passing through the center.
- Chords equidistant from the center are equal in length.
- An angle subtended by an arc at the center is twice the angle subtended at any point on the remaining part of the circle.

Worksheet Solutions

Here are some typical problems you might encounter:
| Problem | Solution |
|---|---|
| Find the length of the arc if the radius is 5 cm, and the central angle is 60 degrees. | Using the formula for arc length L = (θ/360°) × 2πr:L = (60°/360°) × 2 × π × 5 = (1/6) × 10π = (5π/3) cm ≈ 5.24 cm
|
| Determine if chord AB is longer than chord CD if both are 3 cm from the center, and chord AB is 7 cm long. | Chords equidistant from the center are equal in length. Therefore, chord AB and CD are of the same length, approximately 7 cm. |
| Calculate the measure of the angle subtended by an arc of 80 degrees at the circumference. | Since the angle at the circumference is half the angle at the center, it's (80°/2) = 40°. |

🔎 Note: When dealing with arc length, ensure your calculator is in degree mode for angle measures unless otherwise specified.
Advanced Concepts
When you delve deeper, you'll encounter advanced concepts like:
- Inscribed Angles: An angle whose vertex is on the circle and whose sides are chords of the circle. The measure of this angle is half the arc it subtends.
- Cyclic Quadrilaterals: A quadrilateral with all four vertices on the circle. Opposite angles in a cyclic quadrilateral sum to 180 degrees.

Practical Applications

Understanding arcs and chords has practical implications:
- Engineering: Designing curves on roads or tracks where precision in arc length and chord length matters.
- Architecture: For domes, arches, and any curved structures where symmetry and stability are critical.
- Astronomy: Calculating the positions of celestial bodies in the sky based on their arc movement.
Geometry in real life is not just about solving problems on paper but applying these principles to create, design, and understand the world around us.
Conclusion

Exploring arcs and chords has shown us the harmony between curves and lines in circles. From calculating the simple length of an arc to understanding the intricacies of inscribed angles and cyclic quadrilaterals, we've covered both basic and advanced principles. Whether for academic interest or practical applications, this knowledge is invaluable in navigating and creating structures, designs, and solutions in a myriad of fields.
Why do we need to understand arcs and chords?

+
Understanding arcs and chords is essential for fields like architecture, engineering, and design, where precise calculations ensure the stability, efficiency, and aesthetics of structures.
Can the length of an arc be longer than the diameter of the circle?

+
No, the length of any arc cannot exceed the circumference of the circle, which includes the diameter plus the rest of the circle’s edge. The diameter itself is the longest straight-line chord possible within a circle.
What’s the difference between the central angle and an inscribed angle?

+
A central angle has its vertex at the circle’s center, while an inscribed angle has its vertex on the circle itself. The central angle subtended by an arc is twice the measure of the inscribed angle subtended by the same arc.
How can I calculate the area of a sector of a circle?

+
The formula for the area of a sector of a circle is (θ/360°) × πr², where θ is the central angle in degrees and r is the radius of the circle.
What are some tools or software used to work with arcs and chords in geometry?

+
Some popular tools include:
- AutoCAD for drafting and design
- Geogebra for interactive geometry
- SolidWorks for 3D modeling