Free Fall Physics: 1-D Kinematics Worksheet Solutions

Understanding Free Fall in One-Dimensional Kinematics

Free fall is a common scenario in physics where an object is released from rest or thrown vertically under the influence of gravity alone, neglecting air resistance. This phenomenon can be analyzed using one-dimensional kinematics, which focuses on motion in a straight line. Here we’ll explore the fundamentals, equations, and typical problems associated with free fall.
The Basic Principles of Free Fall

In free fall, objects fall towards the Earth at an acceleration commonly denoted as g, where:
- g = 9.8 m/s² on the surface of Earth (for simplicity, we often use 9.8 m/s², but this value can vary slightly based on location and elevation)
- The direction of g is downward, usually taken as negative
The key equations for free fall are:
- v = u + gt (velocity equation)
- s = ut + (1⁄2)gt² (displacement equation)
- v² = u² + 2gs (no time, velocity squared equation)
Here, u is initial velocity, v is final velocity, s is displacement, t is time, and g is the acceleration due to gravity.
Common Free Fall Problems and Solutions
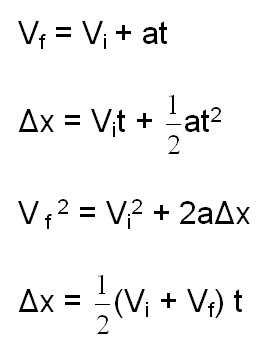
Let’s delve into some typical problems involving free fall:
Problem 1: Object Dropped from Rest

An object is dropped from a height of 100 meters. Find the time taken to reach the ground and its speed just before impact.
- Given:
- u = 0 (since dropped from rest)
- s = 100m (downwards, therefore take as negative)
| Step | Calculation |
|---|---|
| Find time (t) | s = ut + (1/2)gt² -100 = (1/2)(-9.8)t² t² = 20.4082 t ≈ 4.52 seconds |
| Find final velocity (v) | v = u + gt v = 0 + (-9.8) * 4.52 ≈ -44.39 m/s |

⏱️ Note: The time taken for an object to fall depends only on the initial height and the acceleration due to gravity, not on the object's mass.
Problem 2: Object Thrown Upwards

An object is thrown vertically upwards with an initial velocity of 20 m/s. Determine:
- The time taken to reach its maximum height
- The maximum height reached
- The total time in the air before returning to the thrower’s hand
- Given:
- u = 20 m/s (upwards)
- g = -9.8 m/s² (downwards)
| Step | Calculation |
|---|---|
| Time to reach maximum height | When v = 0: v = u + gt 0 = 20 + (-9.8)t t = 2.04 seconds |
| Maximum height reached (h) | v² = u² + 2gh 0² = (20)² + 2(-9.8)h h = -200/(-19.6) ≈ 10.204 meters |
| Total time in air | Time up + Time down = 2 * 2.04 ≈ 4.08 seconds |
Insights into Free Fall Calculations

Free fall problems often involve basic algebra and a clear understanding of the kinematic equations:
- The acceleration due to gravity, g, is constant and acts downwards, affecting all objects uniformly.
- When an object is thrown upwards, its velocity at the peak of its trajectory is zero, and the time to reach this point is half the total time of flight.
- The symmetry in free fall means that an object will take the same amount of time to rise as it does to fall back down to the same height.
In summary, understanding free fall involves:
- Mastery of kinematic equations
- Recognition of the constant acceleration of gravity
- Application of algebraic manipulation to solve for unknowns
📝 Note: Always consider the direction of motion when setting up your equations; in free fall, down is typically negative, but this is a convention and can vary based on problem setup.
To wrap up our exploration, free fall physics not only equips us with the tools to predict the motion of falling objects but also provides a rich understanding of how forces like gravity influence everyday phenomena. As we’ve seen, whether an object is dropped, thrown, or even just left to fall from a high place, the principles of one-dimensional kinematics can guide us through its journey from the sky to the ground.
Why does everything fall at the same rate regardless of mass?

+
In the absence of air resistance, all objects accelerate towards Earth at the same rate because the acceleration due to gravity (g) depends only on the gravitational force and the distance from the center of the Earth, not the mass of the objects. This was famously demonstrated by Galileo’s experiment at the Leaning Tower of Pisa.
Can we achieve zero velocity in free fall?

+
Yes, when an object thrown upwards reaches its peak, its velocity momentarily becomes zero. After that, it starts falling back to Earth with increasing speed.
How does air resistance affect free fall?

+
Air resistance opposes the motion of an object through the air, reducing acceleration and terminal velocity. As a result, objects with a larger surface area relative to their mass will experience more air resistance, falling slower than objects with a smaller surface area.



