5 Acceleration Problems Solved: 1-D Kinematics Worksheet Answers

In the realm of physics, particularly within the study of kinematics, one-dimensional (1-D) motion is foundational. Understanding this concept is crucial as it forms the basis for more complex motion studies, such as two-dimensional projectiles or three-dimensional trajectories. Acceleration, as a derivative of velocity and a second derivative of displacement, plays a pivotal role in deciphering the dynamics of objects in motion. This detailed guide addresses common acceleration problems students face in 1-D kinematics, providing comprehensive solutions to enhance understanding.
Understanding Acceleration in 1-D Kinematics

Acceleration in one-dimensional kinematics refers to how quickly the velocity of an object changes. It can be uniform (constant acceleration) or non-uniform (variable acceleration). Here’s a quick review:
- Uniform Acceleration: When an object’s acceleration does not change with time. Classic examples include free fall under gravity.
- Variable Acceleration: When acceleration changes during the motion. For instance, when a car accelerates from rest to reach a certain speed with varying acceleration.
The most fundamental equations in 1-D kinematics involving acceleration are:
- v = u + at (where v is final velocity, u is initial velocity, a is acceleration, and t is time)
- s = ut + ½ at² (s is displacement)
- v² = u² + 2as
- s = ½ (u + v)t
Problem 1: Acceleration with Initial and Final Velocities
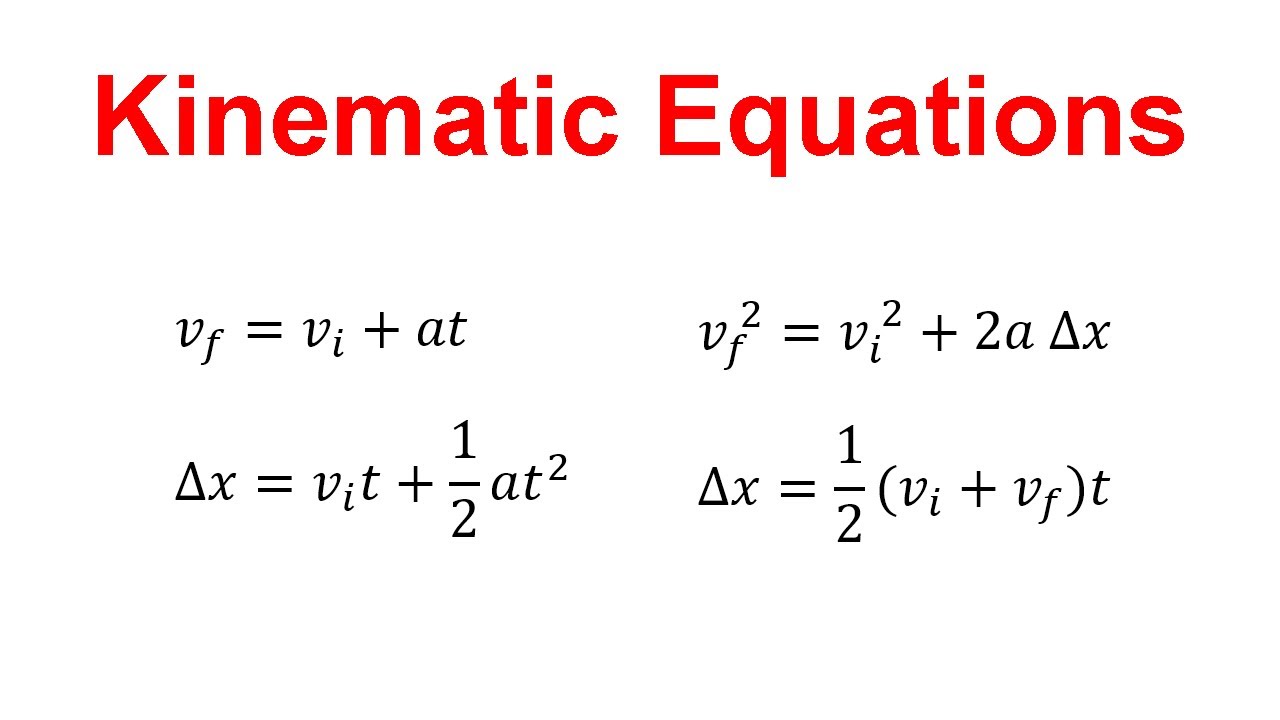
Let’s consider an object starts with an initial velocity of 5 m/s and accelerates to 15 m/s over 3 seconds. What is its acceleration?
Using the equation v = u + at:
- 15 = 5 + (a * 3)
- 10 = 3a
- a = 10⁄3 ≈ 3.33 m/s²
🚀 Note: Keep in mind that when solving kinematic problems, it's vital to check the consistency of units. Acceleration should always be in meters per second squared (m/s²).
Problem 2: Determining Distance with Acceleration

Given an object initially at rest accelerates at 4 m/s² for 8 seconds, how far does it travel?
Using s = ut + ½ at²:
- s = 0 * 8 + ½ * 4 * (8²)
- s = ½ * 4 * 64
- s = 128 meters
Problem 3: Velocity-Time Graphs and Acceleration

An object’s velocity-time graph shows a straight line from (0,0) to (10,20) seconds. Find its acceleration and total displacement.
- Acceleration is the slope of the v-t graph:
- a = (20 - 0)/(10 - 0) = 2 m/s²
- Displacement is the area under the v-t graph:
- s = ½ * (20 - 0) * 10 = 100 meters
Problem 4: Stopping Distance

A car moving at 30 m/s comes to a stop with uniform acceleration in 5 seconds. What is the deceleration, and how far does it travel before stopping?
Using v = u + at for deceleration (a is negative):
- 0 = 30 + a(5)
- a = -30⁄5 = -6 m/s² (deceleration)
Then, using s = ½ (u + v)t:
- s = ½(30 + 0) * 5 = 75 meters
🚗 Note: Deceleration is often referred to as negative acceleration in physics.
Problem 5: Circular Track Motion

A motorcycle travels around a circular track of 100 meters radius. The initial speed is 10 m/s, and after 20 seconds, the speed is 30 m/s. What is the average acceleration?
Given the object is on a circular path, but this scenario simplifies to 1-D kinematics considering only speed changes:
- average acceleration = (30 - 10)/20 = 1 m/s²
| Problem | Initial Condition | Acceleration | Final Condition |
|---|---|---|---|
| 1 | 5 m/s | 3.33 m/s² | 15 m/s |
| 2 | 0 m/s | 4 m/s² | 128 meters |
| 3 | Straight line v-t graph | 2 m/s² | 100 meters |
| 4 | 30 m/s | -6 m/s² | 75 meters |
| 5 | 10 m/s | 1 m/s² | 30 m/s |

In wrapping up this exploration into 1-D kinematics problems, we've touched upon various facets of acceleration from understanding its basic concepts to solving complex problems. These examples illustrate how acceleration, whether it's positive or negative, uniform or variable, is an essential concept in physics. From calculating the deceleration required to bring a car to a stop, to understanding the relationship between acceleration and velocity-time graphs, the principles discussed here are foundational in physics and crucial for deeper learning in mechanics and beyond.
How do I know if acceleration is positive or negative?

+
Acceleration is positive when an object’s velocity increases in the same direction as its initial motion. It’s negative when the velocity decreases or the direction of motion changes due to deceleration.
What’s the difference between speed and velocity?

+
Speed is a scalar quantity that measures how fast an object is moving without regard to direction, whereas velocity is a vector that includes both speed and direction.
Can acceleration be zero while speed is changing?

+
Yes, if an object moves in a circular path with constant speed, its speed remains unchanged, but its velocity (due to direction change) leads to an acceleration directed towards the center of the circular path.